Numerical solution of singular non-linear integral equation

Question

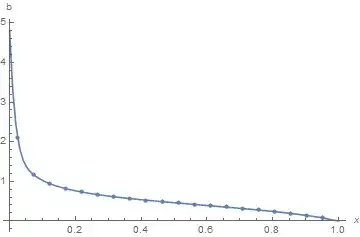
I want to extend this collocation method based mathematica scheme to solve following non-linear integral equation (Cauchy/Carleman type):

$$B(v)/(1-v) \int_{0}^{1} \mathrm{d}x B(x) (1-x)/(v-x) = 1 $$ (eq. 1)

However, all those $1/(v-x)$ are singularities lying right at the collocation points, so the collocation method breaks.

I tried to apply singularity subtraction by solving for a bounded function

$$ A(\zeta)=\int _{0}^{\zeta}(1-v) B(v) dv$$ from which $$B(\zeta)=A^{'}(\zeta)/(1-\zeta)$$ (eq. 2)

This transfomrs eq. (1) into

$$ A^{'}(\zeta) \int_{0}^{1} \frac{A^{'}(\zeta')}{(\zeta-\zeta')} \mathrm{d}\zeta'= (1-\zeta)^2$$ (eq. 3)

to reduce the singularity we use the relation $$\int_{0}^{1} d\zeta' \frac{1}{\zeta'-\zeta}=ln\left(\frac{1-\zeta}{\zeta}\right)$$

and re-write the eq. (3) as

$$ [A'(\zeta)]^2ln\left(\frac{1-\zeta}{\zeta}\right)+A'(\zeta)\int_{0}^{1}\frac{A'(\zeta)-A'(\zeta')}{\zeta-\zeta'} d\zeta'=-(1-\zeta)^2 $$

Now, integral is weakly singular but in terms of collocation method, the term $1/(\zeta-\zeta')$ is still troublesome which leads to 1/0 condition. It would be nice if one could help in extension of above referenced collocation scheme to this integral equation, or any other numerical scheme for solution of eq. (1) or eq. (3).

Answer 1

Edited to improve accuracy at x == 1.

This integral equation can be solved as follows. First, represent b as an InterpolatingPolynomial, in this case with 21 uniformly spaced points, the last of which is b[1] == 0 (which follows directly from the integral equation).

n = 20;
pts = Table[{i, Unique["b"]}, {i, 1/(2 n + 1), 1 - 2/(2 n + 1), 2/(2 n + 1)}];
b = InterpolatingPolynomial[Join[pts, {{1, 0}}], x];

Then, perform the integrations at each point (except b[1]) using the Cauchy principal value.

int = ParallelTable[Integrate[b (1 - x)/(i - x), {x, 0, 1}, PrincipalValue -> True], 
    {i, 1/(2 n + 1), 1 - 2/(2 n + 1), 2/(2 n + 1)}] // N;

and solve for the values of b at those points.

sol = FindRoot[MapThread[Last@#1 #2 == 1 - First@#1 &, {pts, int}], 
    pts /. {z1_, z2_} -> {z2, 1 - z1}]

(* {b17 -> 2.11018, b18 -> 1.16491, b19 -> 0.94366, b20 -> 0.816571, 
    b21 -> 0.730554, b22 -> 0.665021, b23 -> 0.611534, b24 -> 0.565617, 
    b25 -> 0.524675, b26 -> 0.487018, b27 -> 0.451457, b28 -> 0.417071, 
    b29 -> 0.383081, b30 -> 0.348752, b31 -> 0.313317, b32 -> 0.275891, 
    b33 -> 0.235362, b34 -> 0.190208, b35 -> 0.138278, b36 -> 0.0762876} *)

Show[Plot[Evaluate[b[x] /. sol], {x, 0, 1}, MaxRecursion -> 1, AxesOrigin -> {0, 0}, 
    PlotRange -> All, AxesLabel -> {x, "b"}], ListPlot[pts /. sol]]

These results, which are relatively insensitive to the number of points n, suggest that a singularity exists at x == 0. Accuracy perhaps can be improved further by placing more points near x == 0. This computation took about 40 minutes.