Summary
Use the Weights option to LinearModelFit, setting the weights to be inversely proportional to the variances of the error terms.
Theory
This is a standard problem: when the errors in the individual $y$ values are expressed in a way that can be related to their variances, then use weighted least squares with the reciprocal variances as the weights. (Search our sister site Cross Validated for more about this, including references and generalizations.)
Creating realistic data to study
To illustrate, suppose the data are given as vectors $x$ and $y$ with the "errors" expressed either as standard deviations of $y$ or as standard errors of estimate of $y$, or any other quantity that can be interpreted as a fixed, constant multiple of the standard deviations of the $y$. Specifically, the applicable model for these data is
$$y_i = \beta_0 + \beta_1 x_i + \varepsilon_i$$
where $\beta_0$ (the intercept) and $\beta_1$ (the slope) are constants to be estimated, the $\varepsilon_i$ are independent random deviations with mean zero, and $\text{Var}(\varepsilon_i) = \sigma_i^2$ for some given quantities $\sigma_i$ assumed to be known accurately. (The case where all the $\sigma_i$ equal a common unknown constant is the usual linear regression setting.)
In Mathematica we can simulate such data with random number generation. Let's wrap this into a function whose arguments are the amount of data and the slope and intercept. I will make the sizes of the errors vary randomly, but generally they will increase as $x$ increases.
simulate[n_Integer, intercept_: 0, slope_: 0] /; n >= 1 :=
Module[{x, y, errors, sim},
x = Range[n];
errors = RandomReal[GammaDistribution[n, #/(10 n)]] & /@ x;
y = RandomReal[NormalDistribution[intercept + slope x[[#]], errors[[#]]]] & / Range[n];
sim["x"] = x;
sim["y"] = y;
sim["errors"] = errors;
sim
]
Here is a tiny example of its use.
SeedRandom[17];
{x, y, errors} = simulate[16, 50, -2/3][#] & /@ {"x", "y", "errors"};
ListPlot[{y, y + errors, y - errors}, Joined -> {False, True, True},
PlotStyle -> {PointSize[0.015], Thick, Thick},
AxesOrigin -> {0, Min[y - errors]}]
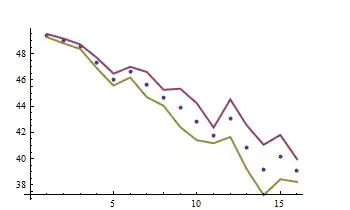
The simulated points are surrounded by error bands.
Weighted least-squares estimation
To fit these data, use the Weights option of LinearModelFit. Once again, let's prepare for later analysis by encapsulating the fitting in a function. For comparison, let's fit the data both with and without the weights.
trial[n_Integer: 1, intercept_: 0, slope_: 0] :=
Module[{x, y, errors, t, fit, fit0},
{x, y, errors} = simulate[n, intercept, slope][#] & /@ {"x", "y", "errors"};
fit = LinearModelFit[y, t, t, Weights -> 1 / errors^2];
fit0 = LinearModelFit[y, t, t];
{fit[#], fit0[#]} & @ "BestFitParameters"
]
The output is a list whose elements give {intercept, slope}: the first element is for the weighted fit, the second for the unweighted.
Monte-Carlo comparison of the weighted and ordinary least squares methods
Let's run a lot of independent trials (say, $1000$ of them for simulated datasets of $n=32$ points each) and compare their results:
SeedRandom[17];
simulation = ParallelTable[trial[32, 20, -1/2], {i, 1, 1000}];
ranges = {{18.5, 22}, {-0.65, -0.35}};
TableForm[
Table[Histogram[simulation[[All, i, j]], ImageSize -> 250,
PlotRange -> {ranges[[j]], Automatic}, Axes -> {True, False}],
{i, 1, 2}, {j, 1, 2}],
TableHeadings -> {{"Weighted", "OLS"}, {"Intercept", "Slope"}}
]
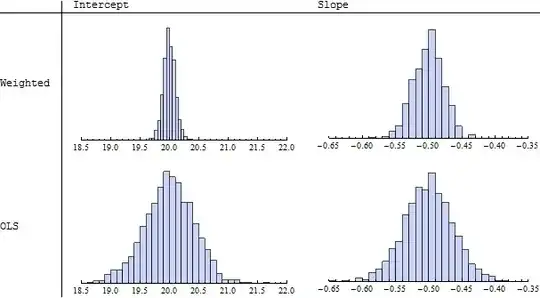
Because I specified an intercept of $20$ and slope of $-1/2$, we will want to use these values as references. Indeed, the histograms in the left column ("Intercept") display sets of estimated intercepts hovering around $20$ and the histograms in the right column ("Slope") display sets of slopes hovering around $-0.50 = -1/2$. This illustrates the theoretical fact that the estimates in either case are unbiased. However, looking more closely at the spreads of the histograms (read the numbers on the horizontal axes), we see that those in the upper row ("Weighted") have smaller widths of their counterparts in the lower row ("OLS," or "Ordinary Least Squares"). This is evidence that the weighted estimates tend, on the whole, to be better then the unweighted ones, because they tend to deviate less from the true parameter values.
When the underlying data truly conform to the hypothesized model--there is a linear relationship between the $x$'s and $y$'s, with errors in the $y$'s having known but differing standard deviations--then among all unbiased linear estimates of the slope and intercept, weighted least squares using reciprocal variances for the weights is best in the sense just illustrated.
Obtaining the estimation error of the slope
Now, to answer the question: we would like to assess the estimation error in the slope. This can be obtained from the fit object in many ways: consult the help page for details. Here is a nicely formatted table:
fit = LinearModelFit[y, t, t, Weights -> 1 / errors^2];
fit0 = LinearModelFit[y, t, t];
TableForm[{{fit[#], fit0[#]} & @ "ParameterConfidenceIntervalTable"},
TableHeadings -> {{}, {"Weighted", "OLS"}}]

In this case, for this particular set of simulated data (as created previously), the weighted method reports a much smaller standard error for the intercept than the OLS method (because errors near $x=0$ are low according to the information in errors) but the weighted estimate of the slope has only a slightly smaller standard error than the OLS estimate of the slope.
Comments
Errors in both $x$ and $y$ can be handled, using--for instance--methods of maximum likelihood. However, this involves considerably more mathematical, statistical, and computational machinery and requires a careful assessment of the nature of those errors (such as whether the $x$ errors and $y$ errors are independent). One general result in the statistical literature is that when the $x$ errors are typically smaller than the $y$ errors, yet independent of them, it is usually safe to ignore the $x$ errors. For more about all this, good search terms include "errors-in-variables regression," "Deming regression," and even "principal components analysis (PCA)".







The most helpful equation in the thread on physicsforums "sigma(slope) = |slope| tan[arccos(R)]/sqr(N-2)" does not seem to take into account uncertainty at all, unless the correlation coefficient R does this somehow?
In addition, I am unsure about the meaning of the function "sqr" and how many degrees of freedom my data has.
– George S Oct 15 '12 at 02:23LinearModelFit[](via itsWeightsoption). – J. M.'s missing motivation Oct 15 '12 at 02:52