By default, Tube has round cross-section (and we define its diameter). Is it possible to draw Tube along some known path in 3D with, e.g. square cross-section?
Thank you.
EDIT
Tried to follow answer from here. I have set of points (just an example, other arcs may have all the coordinates non-zero):
pts = {{0.`, 0.`, 0.`}, {7.497665500157259`*^-14, 0.00036555534709634656`, 0.041887873232098444`}, {2.9988378071419946`*^-13, 0.0014621100333863195`, 0.08376298663421493`}, {6.746528662189823`*^-13, 0.0032893300277940163`, 0.12561258426325045`}, {1.1991697498398906`*^-12, 0.005846658724918654`, 0.16742391794868797`}, {1.8732746539195436`*^-12, 0.009133317114586991`, 0.20918425117592362`}, {2.696762233490476`*^-12, 0.013148304019154402`, 0.25088086296604745`}, {3.669381638827055`*^-12, 0.017890396398482316`, 0.2925010517508915`}, {4.790836591859004`*^-12, 0.02335814972249914`, 0.33403213924216535`}, {6.0607854764232425`*^-12, 0.029549898411231134`, 0.37546147429349974`}, {7.478841442326563`*^-12, 0.03646375634216925`, 0.41677643675422266`}, {9.044572523187444`*^-12, 0.04409761742481735`, 0.45796444131369324`}, {1.0757501768021084`*^-11, 0.052449156242246726`, 0.499012941335023`}, {1.26171073865276`*^-11, 0.06151582875946169`, 0.5399094326770161`}, {1.4622822908039118`*^-11, 0.07129487309836018`, 0.5806414575031648`}, {1.6774037354077335`*^-11, 0.08178331037905351`, 0.6211966080765395`}, {1.9070095424469`*^-11, 0.09297794562728895`, 0.6615625305394178`}, {2.1510297696962602`*^-11, 0.10487536874769866`, 0.7017269286765003`}, {2.4093900840285483`*^-11, 0.11747195556257856`, 0.7416775676605682`}, {2.6820117840576448`*^-11, 0.13076386891588063`, 0.7814022777794407`}, {2.9688118241124915`*^-11, 0.14474705984208247`, 0.8208889581430966`}}
According to that answer first we need to have path in parametric form, to use FrenetSerretSystem. I tried to use Interpolation @ pts, but this gives me error and no result.
Then I attempted to find FindGeometricTransform between successive points in pts and apply these transformation functions to 4 points of initial rectangle (analogue of nlist in that answer). And (sub)-question here: in this my simple example initial point is (0,0,0) and inititial direction is along z-axis, so we choose some 4 points in x-y plain. And what to do in case of arbitrary initial point and direction of arc?
tf = #[[2]] & /@ (FindGeometricTransform[{#[[2]]}, {#[[1]]}] & /@ Partition[pts, 2, 1])
Then I thought I can use BSplineSurface on these computed points, but I get empty Graphics3D object.
bend = Join[ComposeList[tf, {-0.05, -0.05, 0}], ComposeList[tf, {-0.05, 0.05, 0}], ComposeList[tf, {0.05, -0.05, 0}], ComposeList[tf, {0.05, 0.05, 0}]]
Graphics3D[BSplineSurface[bend]]
So, where am I wrong? And can somebody explain in simple steps how to use that answer in my case.
EDIT2
Suppose, we have set of points with arbitrary initial one, as this:
pts1={{4.38673, -4.49861, 5.9078}, {4.36436, -4.52904, 5.93017}, {4.34115, -4.5582, 5.95338}, {4.31716, -4.58604, 5.97737}, {4.29241, -4.61254, 6.00212}, {4.26695, -4.63763, 6.02759}, {4.2408, -4.6613, 6.05373}, {4.21402, -4.6835, 6.08051}, {4.18665, -4.70419, 6.10789}, {4.15872, -4.72334, 6.13582}, {4.13028, -4.74093, 6.16426}, {4.10138, -4.75693, 6.19317}, {4.07205, -4.77131, 6.22249}, {4.04235, -4.78405, 6.2522}, {4.01232, -4.79513, 6.28224}, {3.982, -4.80454, 6.31256}, {3.95144, -4.81225, 6.34311}, {3.9207, -4.81827, 6.37386}, {3.88981, -4.82257, 6.40475}, {3.85882, -4.82515, 6.43574}, {3.82779, -4.82601, 6.46678}}
How to modify functions in answer of SquareOne?
EDIT3
Many thanks to SquareOne and J.M. for helpful comments. Now I can draw pictures like this:
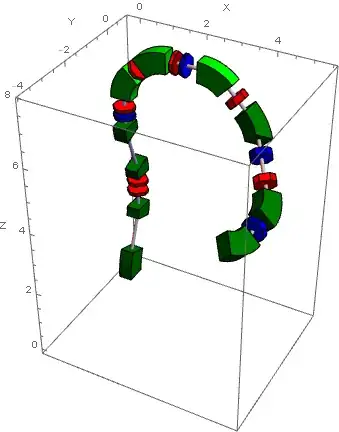
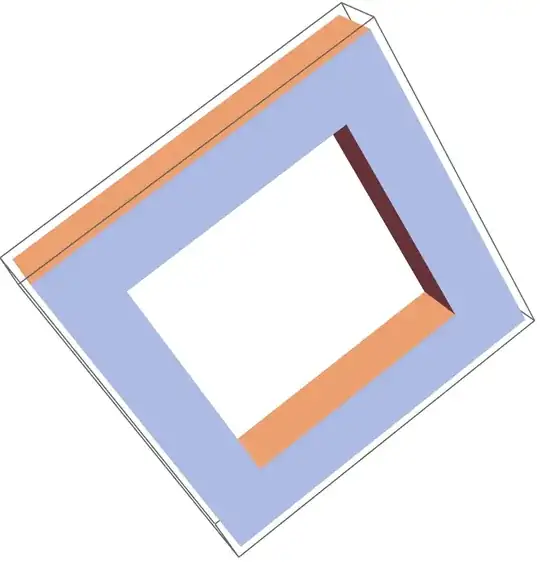
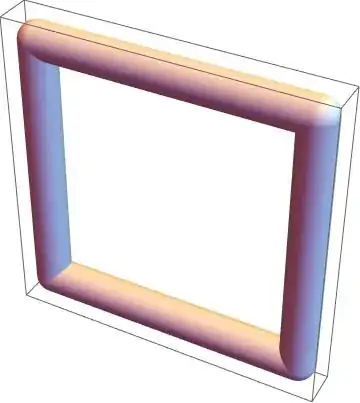
Graphics3D[Tube[BSplineCurve[points],0.7]]. Now I want this object having rectangular cross-section instead of round, as Tube has. In other words one can imaginCuboidbended along 3d arc. – Alx Dec 12 '16 at 02:14Graphics3D[{EdgeForm[], TubePolygons[pts, {{1, 1}, {-1, 1}, {-1, -1}, {1, -1}, {1, 1}}/30, "Normals" -> False]}, Boxed -> False], which uses routines here, yields this. – J. M.'s missing motivation Dec 12 '16 at 10:21ptspath, a very quick and dirty hack is just to replace these definitionspath[u_] := BSplineFunction[#][u] & /@ (Transpose@ Table[BSplineFunction[pts, 1][t], {t, 0, 1, 1/10}]) ; {uStart, uEnd} = {0, 1};. Not guaranteed to work all cases ! Be careful. You may need to adjust1/10to smaller values ... – SquareOne Dec 12 '16 at 12:36ParametricPlot3D[]do the sampling, since uniform sampling might miss details that adaptive sampling won't, unless one uses (often wastefully) small step sizes. – J. M.'s missing motivation Dec 12 '16 at 12:40FrenetSerretSystem[f_BSplineFunction](which is missing)? – SquareOne Dec 12 '16 at 13:09BSplineFunction[], I'd prolly convert it first to an explicit representation in terms ofBSplineBasis[]. – J. M.'s missing motivation Dec 12 '16 at 13:19path[u_] := BSplineFunction[#][u] & /@ (Transpose@ First@Cases[ ParametricPlot3D[BSplineFunction[pts][t] // Evaluate, {t, 0, 1}, MaxRecursion -> 1], Line[l_] :> l, Infinity]); {uStart, uEnd} = {0, 1};. I'll probably modify my post in order to add this. – SquareOne Dec 12 '16 at 13:55path[u]as parametric form of curve to compute tangent, normal and binormal vectors at some point of the curve? I have strange results:tan=D[path[u],u]/.u->0//Normalizegives{2.11809*10^-12, 0.010327, 0.999947}, andnor=D[path[[u],{u,2}]/.u->0//Normalizegives{-1.5662*10^-12, -0.00763613, -0.999971}. I expectnorhas direction parallel toy-axis. – Alx Dec 12 '16 at 16:44frenet[u]usespath[u]to return directly{tangent, normal,binormal}also known as ... Frenet Trihedron. Your formula for normalnoris not valid here becauseuis not the arc length ... see dif. geom. courses. – SquareOne Dec 12 '16 at 20:25path[u]is parametric form of the curve, so decided I can use usual formulae for tangent, normal ... as for{x(t),y(t),z(t)}. One more question. If I have arbitrary first point ofpts, not{0, 0, 0}as in my example, how should I modify your code? Should I replacepath[u]topath[u]-path[0]? – Alx Dec 13 '16 at 02:45