2

I want to plot the real part of function $y(x)$ given by the following implicit equation:

$$[y + (e + f x^2)x^2 + 23 x^2](gy + x^2 + 2 \frac{a}{d^2}\ln\frac{1 - b}{1 - c}) =0,$$

where $a$, $b$, $c$, $d$, $e$, $f$, $g$ are all constant, $y$ is the dependent variable and $x$ is the independent variable with $x\geq0$ in my problem. Inspired by this question and answer, I use FindRoot to do this. The code works, but it gives different curves as the change of start point in FindRoot. Therefore, I am really confused at which curve I should use and why?

First, give all the constants as exact value

a = 13/10; b = 4/10; c = 12/100; d = 10; e = -254; f = 2998; g = 10/79;

Then, define function and Simplify it

eq[x_] := (y + (e + f x^2)*x^2 + 23 x^2)*(g*y + x^2 + 
  2 a*Log[(1 - b)/(1 - c)]*1/d^2) == 0 // Simplify

Next, use FindRoot to obtain the function dependency $y(x)$

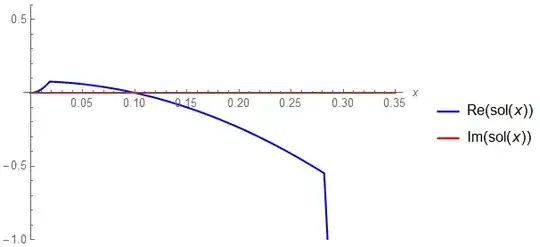
sol[x_?NumericQ] := FindRoot[eq[x], {y, 0}][[1, 2]] (*note the start value, here is 0*)

Last, plot it

Plot[{Re[sol[x]], Im[sol[x]]}, {x, 0, 0.35}, AxesLabel -> {x, None},
PlotLegends -> "Expressions", PlotStyle -> {Blue, Red}, PlotRange -> All]

enter image description here

Question: I found that the curve changes qualitatively with the start point of y, however, it will remain the same if the start value is larger or small than a threshold (here the threshold are 10 and -10, respectively). My question is which of the curves is the true real part and why it changes qualitatively?

If the start point in FindRoot is $10$: sol[x_?NumericQ] := FindRoot[eq[x], {y, 10}][[1, 2]], I will get

enter image description here

Furthermore, if $-10$ as the start point, it gives

enter image description here

And you can even get other different curves. Thank you in advance.

Community
  • 1
lxy
  • 165
  • 5
  • 19
  • Simplify[Reduce[(y+(e+f x^2)x^2+23 x^2)(g y+x^2+2 a/d^2 Log[(1-b)/(1-c)])==0,y]] finds two well behaved Real solutions for y. One of those is making the first half of your left hand side==0 and the other is making the second half of your left hand side==0. That is why you are getting two different solutions. If you plot from x==-.35 to .35 you see a nice symmetric behavior for y. – Bill Dec 13 '16 at 05:03
  • Thanks @Bill, your are right, I understood $y(x)$ is an even function of $x$. Btw, in my problem, I need $x\geq0$. Well, the point is that the implicit equation determines multiple function dependencies with respect to $x$. :) which one I should use? – lxy Dec 13 '16 at 07:28
  • Isn't there any hint in whatever generated that implicit equation on which branch is the "right" one? Take the (inverse) trigonometric functions and angles as a simpler example: one might get either the solution $-2\pi/3$ or $4\pi/3$ (among an infinity of possible solutions) but there may be something in the application concerned that will allow you to choose only one of them. – J. M.'s missing motivation Dec 13 '16 at 07:37
  • Thanks @J.M. I agree with you. However, I don't know to choose which one because (1) I noted that each branch has two sharp turning points when the 'initial value' for FindRoot exceeds the threshold, thus it looks weird due to the non-smoothness, and (2) when the initial value less than the threshold, however, the curve changes with the initial value. – lxy Dec 13 '16 at 07:51
  • I don't know how to tell which of the multiple solutions of your equation is right for you, only you can do that. But you could use this previous answer to plot all of the solutions simultaneously. –  Dec 13 '16 at 16:37
  • There are no "sharp turns", those are where the two solutions are equal and confuse the numeric solver to jump from one solution to the other and thus give you nonsense. See this a=13/10; b=4/10; c=12/100; d=10; e= -254; f=2998; g=10/79; sols = Map[ y/.#&, {ToRules[Reduce[(y+(e+f x^2)x^2+23 x^2)(g y+x^2+2 a/d^2 Log[(1-b)/(1-c)])==0, y]]}]; Print[sols]; Plot[sols,{x,0,.29}, PlotRange->{-.7,1}] to confirm that both solutions are perfectly smooth. – Bill Dec 13 '16 at 21:17
  • See also ContourPlot[(y + (e + f x^2)*x^2 + 23 x^2)*(g*y + x^2 + 2 a*Log[(1 - b)/(1 - c)]*1/d^2) == 0, {x, 0, 0.5}, {y, -2, 5}, MaxRecursion -> 3]: https://i.stack.imgur.com/J8Hxr.png –  Dec 15 '16 at 21:12

0 Answers0