My equation is
I e2 s2 w (m1^2 m2 q1 s1^2 s2 + m1 m2^2 q2 s1^2 s2 + m1^2 q1 s1^2 s2 ζ -
m2^2 q2 s1^2 s2 ζ - 2 m1 q1 s1^2 s2 ζ^2 - m2 q1 s1^2 s2 ζ^2 + m1 q2 s1^2 s2 ζ^2 +
q1 s1^2 s2 ζ^3 - q2 s1^2 s2 ζ^3) +
1/w s1 γ ζ^3 (2 I m2^2 q2 s1 s2^2 ζ + 2 I m2 q1 s1 s2^2 ζ^2 -
2 I m2 q2 s1 s2^2 ζ^2 - 2 I q1 s1 s2^2 ζ^3) -
I (m1^2 m2 q1 s1 s2^2 + m1 m2^2 q2 s1 s2^2 - m1^2 q1 s1 s2^2 ζ + m2^2 q2 s1 s2^2 ζ +
m2 q1 s1 s2^2 ζ^2 - m1 q2 s1 s2^2 ζ^2 - 2 m2 q2 s1 s2^2 ζ^2 - q1 s1 s2^2 ζ^3 +
q2 s1 s2^2 ζ^3) (-e1 s1 w + (s1 γ ζ^3)/w) == 0
and
m1 = Sqrt[ζ^2 - I*w/s1]; m2 = Sqrt[ζ^2 - I*w/s2];
The independent variable is w. All the other variables are constant except ζ (complex number).
q1 = 1; q2 = 0.5; e1 = 1; e2 = 0.8; s1 = 1; s2 = 0.6; γ =1000;
I used FindRoot and solved this problem. FindRoot gives the solution only for one case of w, but I want to plot the graph of w and ζ.
How do I plot Re[ζ] vs.w and Im[ζ] vs. w?
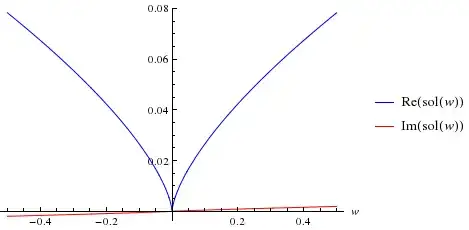
eqs[w_] =andsol[w_?NumericQ] := FindRoot[eqs[w] == 0, {\[Zeta], 1 + I 1/2}][[1, 2]]. – b.gates.you.know.what Sep 15 '13 at 08:21