How to make a random pebble?

Question

I would like to generate a random smooth convex body, like a pebble or a potato (but strictly convex, that's necessary). My attempts:

ConvexHullMesh[RandomReal[1, {10000, 3}], PlotTheme -> "SmoothShading"]

-- clearly bad, too cube-biased;

ConvexHullMesh[ Map[# + RandomReal[.3, 3] &, Flatten[Table[{Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}, {u, -(\[Pi]/2), \[Pi]/2, \[Pi]/100}, {v, -\[Pi], \[Pi], \[Pi]/200}], 1]], PlotTheme -> "SmoothShading"]

-- better, but now too spherical; besides, both not sufficiently smooth.

What would be a scientific approach? What actually is a random smooth convex body?

Thanks, J. M. and @user9490, probably I can use this. Still have to figure out how to make it strictly convex - once there are any concave regions , if I just make a convex hull they will produce something semiconvex, which I want to avoid. — მამუკა ჯიბლაძე, Dec 28 '16 at 17:01
maybe look at this http://mathworld.wolfram.com/Superellipsoid.html — george2079, Dec 28 '16 at 18:22
How fast a solution should be? Do you plan to run the pebble making function a lot of times (say, in a loop) or relatively few pebbles would be sufficient for your plans? — Anton Antonov, Dec 28 '16 at 18:43
@AntonAntonov I only need some static ones, not many. Just point data, although as many points as possible to make it smooth. Or, say, analytic expression, say parametric equations of the surface, although I cannot think in what sense a random one can be given analytically. — მამუკა ჯიბლაძე, Dec 28 '16 at 21:20

Anton Antonov · Accepted Answer · 2016-12-28T23:33:49.870

As mentioned in the comments this answer produces results too slowly and the pebbles are not that smooth, but since I did go through with the idea (which I find interesting) I am posting the outcomes.

The idea for making a random pebble is to generate random points that would determine pebble's shape and then use a 3D quantile envelope to derive pebble's surface.

Here we generate the random points in such a way that they determine the pebble shape:

data1 =
  RandomVariate[
   MultinormalDistribution[{1, 2, 
     3}, {{3, 0, 0}, {0, 1, 0}, {0, 0, 2}}], 1*10^4];

data2 =
  RandomVariate[
   MultinormalDistribution[{1, 2, 2/5}, 
    0.8 {{1, 0, -1/2}, {0, 1, 0}, {-1/2, 0, 2}}], 1*10^4];

data = Join[data1, data2];
Dimensions[data]

(* {20000, 3} *)

Making random variate mixtures with different distributions and parameters (means/centers, variations/correlation matrices) would bring different pebble shapes.

Some additional rotation (optional):

rmat = RotationMatrix[Pi/3., {{1, 1, 1}, {1, -1, 1}}];
data = data.rmat;

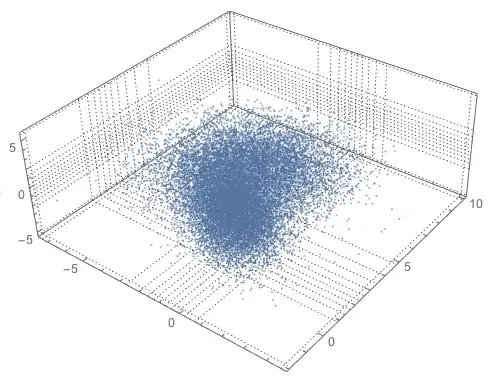
Plot the generated random points:

Block[{qs = 12}, 
  qs = Map[Quantile[#, Range[0, 1, 1/(qs - 1)]] &, Transpose[data]];
  ListPointPlot3D[data, 
  PlotStyle -> {PointSize[0.002]}, PlotRange -> All, 
  PlotTheme -> "Detailed", 
  FaceGrids 
   -> {{{0, 0, -1}, Most[qs]}, {{0, 1, 0}, qs[[{1, 3}]]}, {{-1, 0, 0}, 
     Rest[qs]}}]]

Find the directional quantile envelope:

Import["https://raw.githubusercontent.com/antononcube/MathematicaForPrediction/master/QuantileRegression.m"]
AbsoluteTiming[
 qreg = QuantileEnvelopeRegion[data, 0.95, 78];
]

(* {4.57647, Null} *)

Discretize the obtained region in order to plot it:

AbsoluteTiming[
 bdreg = BoundaryDiscretizeRegion[qreg];
]

(* {168.562, Null} *)

The command above will take less time if smaller number of directions in QuantileEnvelopeRegion are used. (The third argument.) The obtained pebble might have some very flat, angular sides.

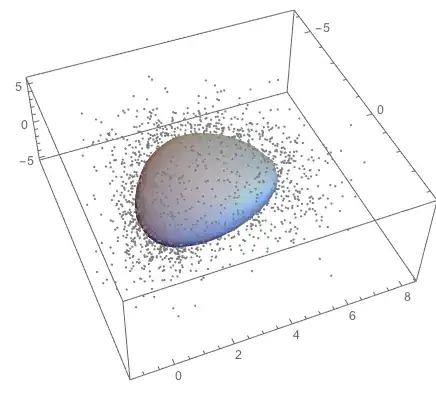
Plot together with a sample of the points:

Block[{testData = RandomSample[data, 4000]},
 Show[{ListPointPlot3D[testData, 
    PlotStyle -> {Gray, PointSize[0.006]}], bdreg}]]

Just the pebble by itself:

bdreg

Probably some further refinements or manipulations of the obtained discretized region can be made in order to derive smoother surfaces.

Yes very interesting idea! I think I will accept it, except that I want to understand better your QuantileEnvelopeRegion function. I found your very nice description, but could you also provide some pointers to a theory underlying it? — მამუკა ჯიბლაძე, Dec 29 '16 at 07:04
@მამუკაჯიბლაძე "Yes very interesting idea! " -- Thanks! I think the theory behind the quantile envelope derivation is fairly well explained in 2D in the blog post "Directional quantile envelopes". The blog post you referred to, "Directional quantile envelopes in 3D", extends that approach in 3D using Mathematica's region functions. — Anton Antonov, Dec 29 '16 at 14:02
@მამუკაჯიბლაძე (cont.) One of the references in the mentioned blog posts is the article "Quantile tomography: using quantiles with multivariate data" which can provide further theoretical background. — Anton Antonov, Dec 29 '16 at 14:07

Greg Hurst · Answer 2 · 2021-06-25T14:06:44.847

7

Another approach is to refine a coarse mesh with multiple iterations of Loop subdivision. One such implementation is here.

SeedRandom[123];
init = ConvexHullMesh[RandomReal[{-1, 1}, {8, 3}]];
BoundaryMeshRegion[init, MeshCellStyle -> {1 -> Black}]

Nest[LoopSubdivide, init, 6]

edited Jun 25 '21 at 14:06

answered Jun 25 '21 at 13:16

Greg Hurst

35,921
1
90
136

Thank you, it is definitely very efficient! Except that I don't really understand what the code is doing. For example, if it tries to approximate the existing polyhedron with a smooth shape, then it is not quite what is needed. A realistic approach would rather shrink the initial shape, similarly to the fact that, to obtain a pebble from a piece of rock, several pieces must break out. But maybe after all the final result is similar, I don't know. – მამუკა ჯიბლაძე Jun 25 '21 at 17:43

score 4 · Answer 3 · answered Jun 25 '21 at 06:53

Although there is an accepted answer, let me describe another approach which I stumbled upon on mathoverflow, in form of the question about "derived" polyhedra there.

Start with a random collection of points in 3d; form convex hull; take barycenters of faces; iterate.

Seems like after about ten iterations a reasonably realistic pebble is obtained, even if one starts with an almost regular system of points initially.

subd[mesh_] := With[
 {vertices = MeshCoordinates[mesh], triangles = Map[First, MeshCells[mesh, 2]]}, 
 ConvexHullMesh[Map[Mean[vertices[[#]]] &, triangles]]
]
trim[mesh_, M_] := Nest[subd, mesh, M]

An example: start with

initmesh = ConvexHullMesh[
  {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}, {-.0001, -.000002, -.000000004}, {-.000000000005, 0, -.1}}
]

Then trim[initmesh, 10] produces

I like this version since it sort of imitates the process by which pebbles are actually formed.

Another (either good or bad, depending on what you need from it) feature of this method is that it seems to be extremely sensitive to initial conditions. In my experiments, changing one of the initial coordinates by about one trillionth resulted in quite different final result.

kglr · Answer 4 · 2021-06-26T13:43:45.433

3

An alternative implementation of the idea in მამუკაჯიბლაძე's answer:

abrade = Nest[ConvexHullMesh[PropertyValue[{#, 2}, MeshCellCentroid]] &, #, #2] &;

Examples:

abrade[ConvexHullMesh[{{1, 0, 0}, {0, 1, 0}, {0, 0, 1}, 
   {-.0001, -.000002, -.000000004}, {-.000000000005, 0, -.1}}], 10]

SeedRandom[1];
abrade[ConvexHullMesh[RandomReal[1, {10, 3}]], 10]

edited Jun 26 '21 at 13:43

answered Jun 26 '21 at 13:07

kglr

394,356
18
477
896

How to make a random pebble?

4 Answers4

Linked