7

I use Mathematica's built-in method:

s1 = NDSolve[{x1'[t] == x2[t], 
x2'[t] == -5 x2[t] - 44 y1[t] - 0.5 x1[t] y1[t] + Sin[5 t], 
y1'[t] == y2[t], 
y2'[t] == -3 y2[t] - 2 x2[t] + x1[t] y1[t]^2 + Cos[5 t], 
x1[0] == 0.1, x2[0] == 0.02, y1[0] == 0.2, y2[0] == 0.01}, {x1, 
x2, y1, y2}, {t, 20}];

I then plot the results and all looks good:

Plot[Evaluate[{x1[t], x2[t], y1[t], y2[t]} /. First[s1]], {t, 0, 20}, 
    PlotLegends -> Placed["x1[t],x2[t],x3[t],x4[t]", Below], PlotRange -> All]

Now, I want to use a Runga-Kutta-Fehlberg Coefficient Plug-in using the documented example. We define the plug-in paramters

Fehlbergamat = {{1/4}, {3/32, 9/32}, {1932/2197, -7200/2197, 
7296/2197}, {439/216, -8, 3680/513, -845/4104}, {-8/27, 
2, -3544/2565, 1859/4104, -11/40}};
Fehlbergbvec = {25/216, 0, 1408/2565, 2197/4104, -1/5, 0};
Fehlbergcvec = {1/4, 3/8, 12/13, 1, 1/2};
Fehlbergevec = {-1/360, 0, 128/4275, 2197/75240, -1/50, -2/55};
FehlbergCoefficients[4, p_] := 
 N[{Fehlbergamat, Fehlbergbvec, Fehlbergcvec, Fehlbergevec}, p];

Fehlberg45 = {"ExplicitRungeKutta", 
   "Coefficients" -> FehlbergCoefficients, "DifferenceOrder" -> 4, 
   "EmbeddedDifferenceOrder" -> 5, "StiffnessTest" -> False};

We then call NDSolve using this plug-in:

 s2 = NDSolve[{x1'[t] == x2[t], 
x2'[t] == -5 x2[t] - 44 y1[t] - 0.5 x1[t] y1[t] + Sin[5 t], 
y1'[t] == y2[t], 
y2'[t] == -3 y2[t] - 2 x2[t] + x1[t] y1[t]^2 + Cos[5 t], 
x1[0] == 0.1, x2[0] == 0.02, y1[0] == 0.2, y2[0] == 0.01}, {x1, 
x2, y1, y2}, {t, 20}, Method -> Fehlberg45];

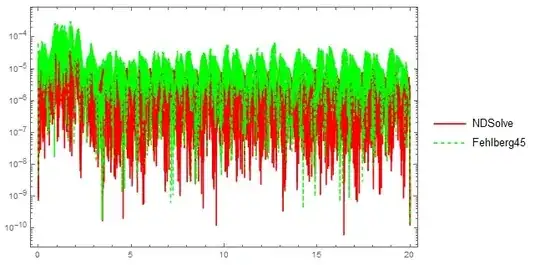
I compared the Mathematica output with this plug-in using a plot of the results, for example

Plot[Evaluate[{x1[t], x2[t], y1[t], y2[t]} /. First[s2]], {t, 0, 20}, 
 PlotLegends -> Placed["x1[t],x2[t],x3[t],x4[t]", Below], 
 PlotRange -> All]

It runs, but when I plot or compare numerical values to Mathematica, the results look identical, thus I am not sure it is working properly. Is there a way to check that indeed the Fehlberg plug-in method is working properly?

Note: this is only tangentially related to this excellent answer Calculating the error in the solution of a system of ODEs, but compare that answer to this one - they are very different.

Community
  • 1
Moo
  • 3,260
  • 1
  • 12
  • 28
  • 2
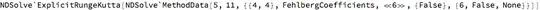
    You can add a Sow[]to the right hand side of FehlbergCoefficients[] and wrap the NDSolvecall in Reap to check if FehlbergCoefficients[] got called. You can also give it \[Rho] as parameter to see with whch arguments it got called. Also have a look at EvaluationMonitor in the documentation. This might help to get a look into the internal calls of NDSolve – Thies Heidecke Jan 22 '17 at 10:01
  • 1
    Just saw the documentation on StepMonitor also has great examples (see the Applications section). – Thies Heidecke Jan 22 '17 at 10:07
  • 4
    If you use StepDataPlot[] to look at the steps taken, you'll see that the behavior of the default multistep method is markedly different from the Fehlberg method. That at least tells us that the default is not being used in the second case. – J. M.'s missing motivation Jan 22 '17 at 10:15
  • 1
    The easiest way to see the difference between the default method and Fehlberg method is to check Plot[Evaluate[MapThread[#[t] - #2@t &, #[[1, All, -1]] & /@ {s1, s2}]], {t, 0, 20}, PlotRange -> All]. – xzczd Jan 23 '17 at 04:10

2 Answers2

5

Ways to get information about an ODE solution sol = NDSolve[..., {x,..}, {t, a, b}]:

  • Steps:
    • x["Grid"] /. sol
    • x["Coordinates"] /. sol
    • Reap[NDSolve[..., StepMonitor :> Sow[t]]
  • Method:
    • Reap[NDSolve[..., MethodMonitor :> Sow[NDSolve`Self]]
    • Trace[NDSolve[...], NDSolve`InitializeMethod[__], TraceInternal -> True]
  • Evaluations:
    • Reap[NDSolve[..., EvaluationMonitor :> Sow[t]]

Example (OP's but with a shorter interval of integration):

Block[{nstep = 0, neval = 0},
  {sol2, {steps2, methods2, eval2}} = 
   Reap[NDSolve[{x1'[t] == x2[t], 
      x2'[t] == -5 x2[t] - 44 y1[t] - 0.5 x1[t] y1[t] + Sin[5 t], 
      y1'[t] == y2[t], 
      y2'[t] == -3 y2[t] - 2 x2[t] + x1[t] y1[t]^2 + Cos[5 t], 
      x1[0] == 0.1, x2[0] == 0.02, y1[0] == 0.2, y2[0] == 0.01},
     {x1, x2, y1, y2}, {t, 0.1},
     Method -> Fehlberg45,
     StepMonitor :> (Sow[{++nstep, t}, "Step"];),
     "MethodMonitor" :> (Sow[NDSolve`Self, "Method"];),
     EvaluationMonitor :> (Sow[{++neval, nstep, t}, "Evaluation"];), 
     MaxStepFraction -> 1],    (* allow longer steps because of short interval *)
    {"Step", "Method", "Evaluation"}]
  ];

A presentations of the steps & evaluation times:

Grid[
 Join[
  {{"Step", "Evaluations", SpanFromLeft}},
  MapIndexed[Join[#2, #1] &,
   SplitBy[First@eval2, #[[2]] &][[All, All, 3]]]
  ],
 Alignment -> {Left, Automatic}]

Mathematica graphics

methods2[[1, 1]] // Short

Mathematica graphics

x1["Grid"] /. sol2
(*{{{0.},{0.0115275},{0.0280347},{0.0448688},{0.0620601},{0.0795363}, {0.0897682},{0.1}}}*)

Note that the default method "LSODA" does not use "MethodMonitor". Use Trace[] to see the NDSolve`LSODA method object it uses.

References:

Community
  • 1
Michael E2
  • 235,386
  • 17
  • 334
  • 747
3

It can be done by comparing the Residual error in both approaches. For this we need to set up the problem like this,

sys = {x1'[t] == x2[t], 
   x2'[t] == -5 x2[t] - 44 y1[t] - 0.5 x1[t] y1[t] + Sin[5 t], 
   y1'[t] == y2[t], 
   y2'[t] == -3 y2[t] - 2 x2[t] + x1[t] y1[t]^2 + Cos[5 t]};
residuals = sys /. Equal -> Subtract;

Now comparing the errors in both methods,

LogPlot[Join[Abs[residuals /. s1], Abs[residuals /. s2]] //Evaluate, {t, 0, 20}, 
PlotStyle -> {Red, Directive[Dashed, Green]},PlotLegends -> {"NDSolve", "Fehlberg45"},
Frame -> True,PlotRange -> All]

enter image description here

Checking the residual error in Fehlberg45 only

LogPlot[Abs[residuals /. s2] // Evaluate, {t, 0, 20},PlotStyle -> Opacity[0.75],
 Frame -> True]

enter image description here

The idea behind this answer can be found here.

Community
  • 1
zhk
  • 11,939
  • 1
  • 22
  • 38