1

The goal is to draw the solution of $y'(t)=y(t)^2-t,\ y(0)=3$, over the region $\{(t,y): -2\le t\le 10,\ -4\le y\le 4\}$. I've started with:

Clear[f, t]
f[t_, y_] := y^2 - t
vp = VectorPlot[{1, f[t, y]}, {t, -2, 10}, {y, -4, 4},
  VectorScale -> {0.03, 0.03, None},
  Frame -> False, Axes -> True, AxesLabel -> {"t", "y"}]

Which gives this image:

enter image description here

Then I tried:

sol = DSolveValue[{y'[t] == y[t]^2 - t, y[0] == 3}, y, t]

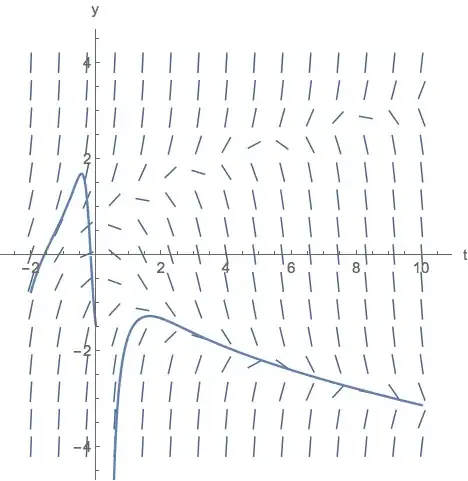
Which gives a weird complex solution. I tried adding it to my direction field.

Show[vp, Plot[sol[t], {t, -2, 10}]]

Which gives this image:

enter image description here

Notice that it does not satisfy the initial condition $y(0)=3$. Then I tried:

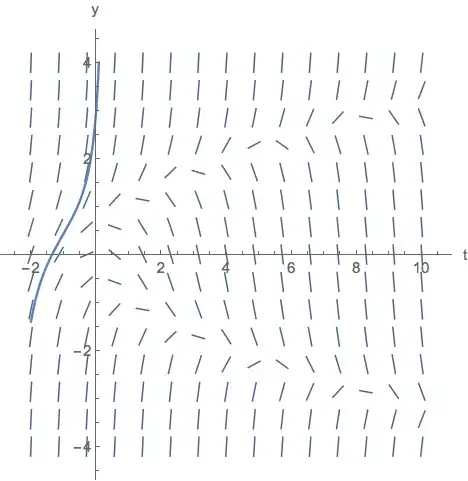
Show[vp, Plot[Re[sol[t]], {t, -2, 10}]]

Which produces this image:

enter image description here

Again, it does not satisfy the initial condition $y(0)=3$. What am I doing wrong? Am I making some type of mistake?

Update: I've managed to find an old discussion How should I deal with messages being produced by my Manipulate? which provides some help.

Clear[f, t]
f[t_, y_] := y^2 - t
vp = VectorPlot[{1, f[t, y]}, {t, -2, 10}, {y, -4, 4}, 
  VectorScale -> {0.03, 0.03, None}, Frame -> False, Axes -> True, 
  AxesLabel -> {"t", "y"}];
sol = NDSolveValue[{y'[t] == y[t]^2 - t, y[0] == 3, 
    WhenEvent[Abs[y[t]] > 4, "StopIntegration"]}, y, {t, -2, 2},
   "ExtrapolationHandler" -> {Indeterminate &, 
     "WarningMessage" -> False}];
Show[vp, Plot[sol[t], {t, -2, 10}]]

Which produces this image.

enter image description here

Which is correct. Also, note that

sol[0]

produces the answer 3.

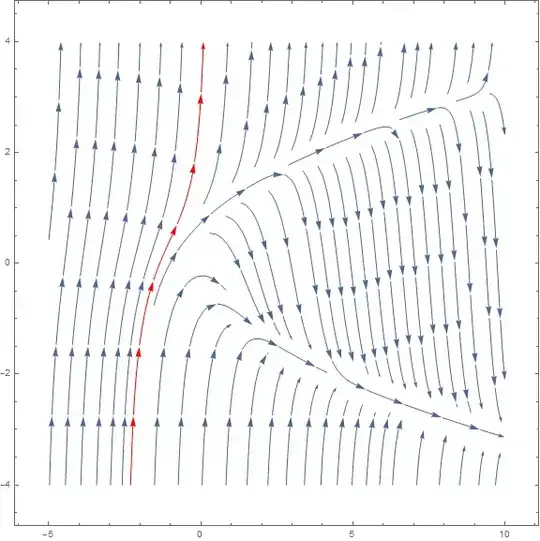
I was also able to do this:

tbl = Table[
   NDSolveValue[{y'[t] == y[t]^2 - t, y[0] == b, 
     WhenEvent[Abs[y[t]] > 4, "StopIntegration"]}, y[t], {t, -2, 10},
    Method -> "StiffnessSwitching",
    "ExtrapolationHandler" -> {Indeterminate &, 
      "WarningMessage" -> False}], {b, -3, 3}];
Show[vp, Plot[tbl, {t, -2, 10}]]

Which produced this image.

enter image description here

However, a good question to still ask is about the ExtrapolationHandler. Could not find it in the documentation. Is it something that will continue to exist?

Community
  • 1
David
  • 14,883
  • 4
  • 44
  • 117
  • 1
    I tried it in maple and it gives solution in terms of Airy. $y \left( t \right) =-{\frac {{\it _C1},{{\rm Ai}^{(1)}\left(t \right)}+{{\rm Bi}^{(1)}\left(t\right)}}{{\it _C1},{{\rm Ai}\left(t \right)}+{{\rm Bi}\left(t\right)}}} $. The numerical solution in maple satisfies the initial condition. – zhk Jan 24 '17 at 12:37
  • Re ExtrapolationHandler, have you tried searching the site?? – Michael E2 Jan 24 '17 at 18:14
  • @MichaelE2 Yes, there are lots of examples (some too advanced for me) on the site that I found helpful, particularly the one I put in the update to my original post, where you made some really helpful explanation. I just could not find ExtrapolationHandler in the Mathematica documentation helper. – David Jan 24 '17 at 22:27
  • I first learned of it in this comment. But "ExtrapolationHandler" seems to have nothing to do with the original question. Whether or not it might be closed as a duplicate, it probably is more viable as a separate question, as discussed on meta here and here. – Michael E2 Jan 24 '17 at 22:42

2 Answers2

3

It's a Plot peculiarity you can fix by giving an explicit PlotRange. For example, try

Plot[sol[t], {t, 0, 10}, PlotRange -> {{0, 2}, {-10, 10}}]
Pirx
  • 4,139
  • 12
  • 37
2

Why not just use StreamPlot?

   StreamPlot[{1,y^2-t},{t,-5,10},{y,-4,4},StreamPoints->    
      {{{{0,3},Red},Automatic}},ImageSize->Large]

enter image description here

Moo
  • 3,260
  • 1
  • 12
  • 28