I have made a knockoff of John Polking's dfield for a web-embedded CDF (via Enterprise Mathematica). My code extends that from Belisarius who last year showed me how to use ClickPane to store and clear solution curves.
Although clicking on any point of the slope field produces an apparently correct solution curve, an error message NDSolve::ndsz is generated by NDSolve. Moreover, by choosing an initial value near the point with coordinates (2,-2) and following by moving the "b" slide from its default position, the slope field turns the color pink and I get the message "InterpolatingFunction::dmval: Input value {-1.99992} lies outside the range of data in the interpolating function. Extrapolation will be used."
sf :=
VectorPlot[{1, diffEq /. {a -> A, b -> B}}, {t, -2, 2}, {x, -2, 2},
VectorPoints -> 17,
VectorScale -> {0.03, Automatic, None},
VectorStyle -> {{Red, Arrowheads[0]}}, ImagePadding -> 1,
PerformanceGoal -> "Speed"];
f[t_, a_, b_, t0_, x0_] :=
u[t] /. First[Quiet[NDSolve[{u'[t] == ODE, u[t0] == x0}, u, {t, -2, 2},
Method -> "StiffnessSwitching"]]];
Manipulate[
ODE = diffEq /. {a -> A, b -> B} /. x -> u[t];
ClickPane[
Show[
Plot[g, {t, -2, 2},
PlotRange -> 2, Frame -> True,
ImageSize -> 400, AspectRatio -> 0.75],
sf,
Graphics[{PointSize[Large], Point[sp]}]],
(AppendTo[g, f[t, A, B, #[[1]], #[[2]]]]; {t0, u0} = #;
AppendTo[sp, #]) &],
Style["Enter f(t,x)"],
{{diffEq, x^2 - a t + b, "dx/dt = "}},
{{A, 1, "a"}, -4, 4, 0.01, Appearance -> "Labeled", ControlPlacement -> Bottom},
{{B, 0, "b"}, -4, 4, 0.01, Appearance -> "Labeled", ControlPlacement -> Bottom},
Button["clear", {g = {}; sp = {}}, ImageSize -> {40, 20}],
Initialization :> {(
g = {}; sp = {}; {t0, x0} = {})},
SaveDefinitions -> True]
FYI, the ODE that I have set as an input is the default used in dfield.
The two error messages that I get are probably related.
NDSolve::ndsz: At t == -1.71226, step size is effectively zero; singularity or stiff system suspected. >>
InterpolatingFunction::dmval: Input value {-1.99992} lies outside the range of data in the interpolating function. Extrapolation will be used. >>
I do not have sufficient Mathematica chops to fix my problem.

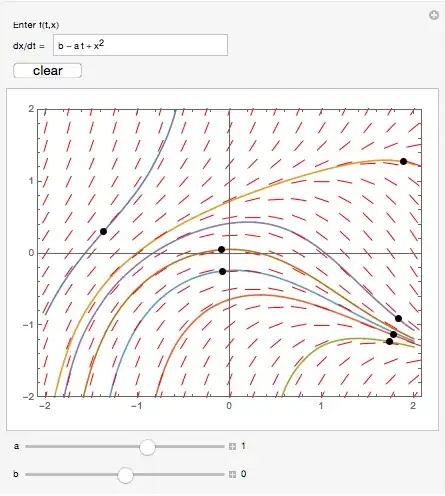
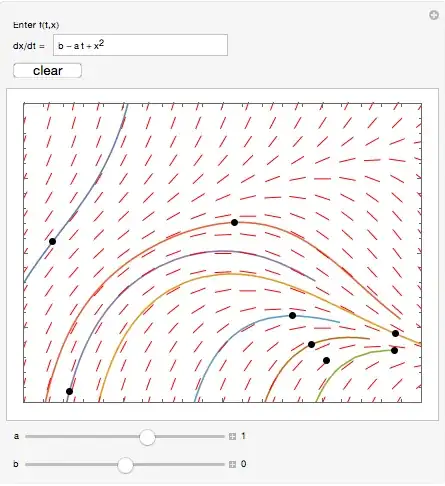
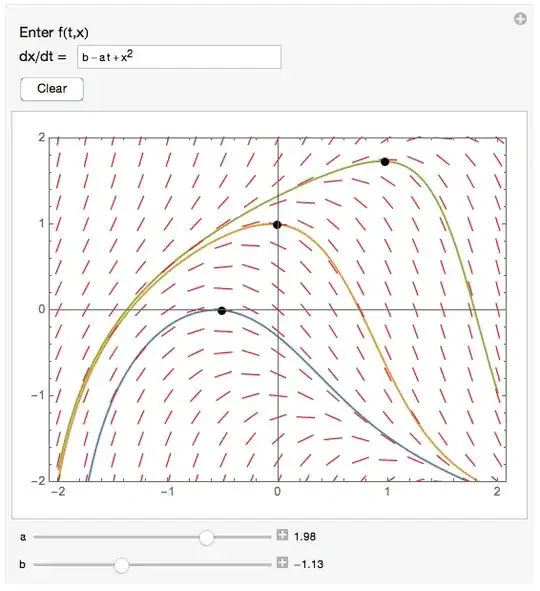

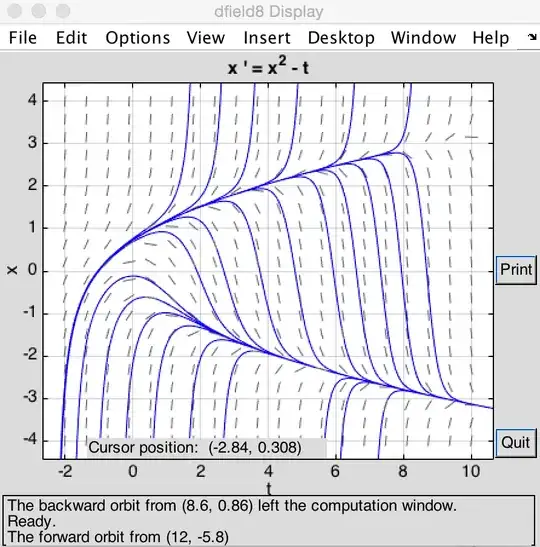
NDSolve::ndszmessage is technically a warning, not an error. It may just be telling you that there is a singularity, which is not an error. (2) You mention error in the singular at first and two errors at the end. Are they the same error? (3) What do the slidersaandbdo? (4) Look upQuiet. There are other ways to handle the message, but I'm not sure I understand the question well enough yet. (5) I added the message identifier based on the text in your title. It helps others who get the same message. If you're getting two different messages, consider adding that one, too. – Michael E2 Aug 13 '15 at 13:07NDSolve. The other is produced byInterpolatingFunctionwhenfis being plotted. – m_goldberg Aug 13 '15 at 13:51NDSolve::ndszerror, only the extrapolation error. Can you specify a setting foraandb? Or did you use a differentf[x, t]? (If you allow arbitrary input forf, you are going to get "bad" ODEs. How do you want to handle such cases that produce messages?) – Michael E2 Aug 13 '15 at 13:59