Why doesn't FindClusters find any clusters in this case?

Question

I am trying to use FindClusters to segment data points into similar numbers but so far I couldn't get it work for this example:

l = {110, 111, 115, 117, 251, 254, 254, 259, 399, 400, 401, 
     402, 542, 546, 549, 554, 660, 660, 660, 660};
FindClusters[l]
(*
-> {{110, 111, 115, 117, 251, 254, 254, 259, 399, 400, 401, 402, 542, 
   546, 549, 554, 660, 660, 660, 660}}
*)

If I set the N parameter (to specify: Exactly N clusters), it works:

FindClusters[l, 5]
(*
-> {{110, 111, 115, 117}, {251, 254, 254, 259}, 
    {399, 400, 401, 402}, {542, 546, 549, 554}, {660, 660, 660, 660}}
*)

However, my intent was to use FindClusters to figure out N.

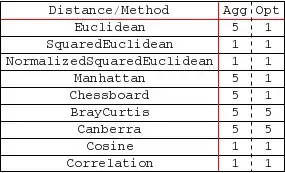
You've tried playing around with various DistanceFunction settings? DistanceFunction -> BrayCurtisDistance and DistanceFunction -> CanberraDistance work here, for instance... — J. M.'s missing motivation, Oct 27 '12 at 17:10
@bel, no prob, though I have a feeling we got lucky, and these only work for the particular case that OP presented, since OP says nothing more about the nature of the actual data... — J. M.'s missing motivation, Oct 27 '12 at 17:15
Thanks for your answers! I am still trying to figure out why EuclideanDistance doesn't work in this case. @J.M.: context is a an OCR algorithm I am trying to implement. I am trying to normalize a grid that has been estimated by WatershedComponents (See my other question) . It's probably too complex to include here. — Sven K, Oct 27 '12 at 17:45
@SvenK Image processing in Mma is quite powerful. Perhaps you don't need to use FindClusters[]. Mind to share more details? — Dr. belisarius, Oct 27 '12 at 17:51
@belisarius AFAIU the problem is that WatershedComponents/ImageTake don't really allow accessing the "bitmap" of a component, so I am using "BoundingBox" but the box is including parts of other characters, so I wanted to smooth the boundingboxes before calling ImageTake. Code example:
i = Import["http://i.stack.imgur.com/Ta5wf.png"] ws = WatershedComponents[i]; ColorCombine[{Image[mc, "Bit"], i, i}] ImageTake[i, Sequence @@ Reverse@Transpose@Last[#]] & /@

ComponentMeasurements[ws, "BoundingBox"] — Sven K, Oct 27 '12 at 18:04
Sorry, it seems the code formatting described in the help for comment formatting doesn't work. — Sven K, Oct 27 '12 at 18:08
@belisarius I created a gist for the example: https://gist.github.com/3965569 — Sven K, Oct 27 '12 at 18:16
@SvenK Try mc = MorphologicalComponents@ColorNegate@i; p = Position[mc, #] & /@ Range@Max@mc; ColorNegate /@ Image /@ (SparseArray[# -> 1 & /@ Transpose[# - Min@# + 1 & /@ Transpose@#]] & /@ p) — Dr. belisarius, Oct 27 '12 at 20:44
@SvenK Do you have measure for the degree of fit for the number of clusters found ? — image_doctor, Oct 28 '12 at 17:27
@image_doctor No, there seems to be no indication as to how well the data could be fitted into clusters, which seems a bit strange. — Sven K, Oct 28 '12 at 18:54

score 8 · Accepted Answer · edited Oct 28 '12 at 02:29

Use the Bray-Curtis distance Total[Abs[u-v]]/Total[Abs[u+v]]:

FindClusters[{110, 111, 115, 117, 251, 254, 254, 259, 399, 400, 401, 
              402, 542, 546, 549, 554, 660, 660, 660, 660}, 
              DistanceFunction -> BrayCurtisDistance]
(*
{{110, 111, 115, 117}, 
 {251, 254, 254, 259}, 
 {399, 400, 401, 402},
 {542, 546, 549, 554}, 
 {660, 660, 660, 660}}
*)

Edit:

Here you have an experimental setup to test the FindClusters[] options in problems like yours:

l1 = RandomInteger[{100, 1000}, 10];
l2 = Join @@ (IntegerPart /@ RandomVariate[NormalDistribution[#, 10], 10] & /@ l1);
l3 = FindClusters[l2, DistanceFunction -> CanberraDistance];
Framed@Show[MapIndexed[
            Graphics[{ColorData[3][#2[[1]]],
                     Line[{{#, 0}, {#, 1}}] & /@ #1}] &, l3], 
            PlotRange -> {0, 1}, AspectRatio -> 1/5]

Mathematica graphics

Neat addition. :) OP should now be able to play around with the Method and DistanceFunction options easily, to see what suits his data best. — J. M.'s missing motivation, Oct 27 '12 at 17:39

image_doctor · Answer 2 · 2012-10-28T19:54:05.033

I'm not really sure why the default option for FindClusters with EuclideanDistance and Method->"Optimize" fails to distinguish any clusters.

Here are some results which might add a little detail:

Here are the numeric distance functions:

dfs = {EuclideanDistance, SquaredEuclideanDistance, NormalizedSquaredEuclideanDistance, 
ManhattanDistance, ChessboardDistance, BrayCurtisDistance, CanberraDistance, 
CosineDistance, CorrelationDistance}

Applying the various distance functions and methods:

Length@FindClusters[l, DistanceFunction -> #, Method -> "Agglomerate"] & /@ dfs
Length@FindClusters[l, DistanceFunction -> #, Method -> "Optimize"] & /@ dfs

{5, 1, 1, 5, 5, 5, 5, 1, 1} {1, 1, 1, 1, 1, 5, 5, 1, 1}

And in tabular form:

Mathematica graphics

So it is possible to use the EuclideanDistance function for this data, but only with agglomerative clustering.

Why doesn't FindClusters find any clusters in this case?

2 Answers2