Degradation of image when used as texture in 3D graphics

Question

An answer at zhihu motivated me to ask this question:

Though applying a texture to a surface or a Graphics object is quite convenient in Mathematica, the quality is a bit low. So the question is straight foward: how do I get the texture on 3-D plots to be of higher quality?

Test code:

img = Texture[
   Graphics[Table[Disk[{j, i}, Sqrt[i]/6], {i, 25}, {j, 50}], 
     PlotRange -> {{1, 50}, {-5, 25}}, ImageSize -> 1000] // 
    Rasterize];
SphericalPlot3D[1, {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> None, 
 TextureCoordinateFunction -> ({#5, #4} &), PlotStyle -> img, 
 Lighting -> {{"Ambient", White}}]

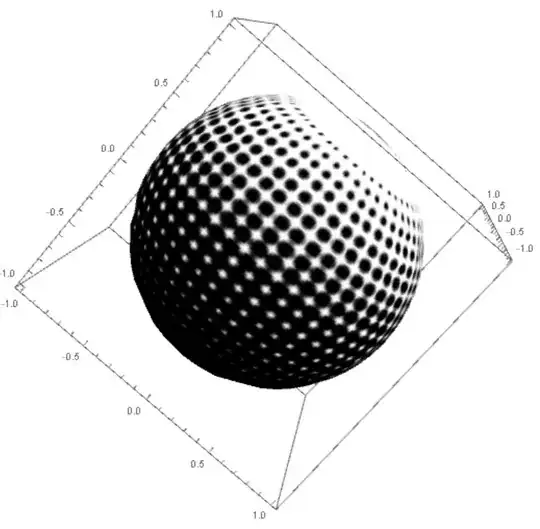
Result generated by test code:

One can see that graphic used as a source for the texture is quite clear while the final result is not satisfying, in particular, the edge is not sharp enough. How to improve the quality of the result?

I think this problem may have come up before but I cannot find it. @Jens the edges in the texture itself, i.e. the transition between black and white. The whole texture looks blurry rather than crisp. I have a vague memory that someone solved this by splitting a surface into multiple Texture regions. — Mr.Wizard, Feb 11 '17 at 06:23
@Mr.Wizard Thanks for your extra explanation! :) I'm curious about why splitting texture will help, what is the mechanism behind this texture applying process? — Wjx, Feb 11 '17 at 06:27
I was simply misremembering, probably influenced by this question:(44863) — Mr.Wizard, Feb 11 '17 at 06:29
First time here. Nice solutions presented. I have been able to save these texture objects (via Export command) in both obj and dae formats but am having trouble when trying to see them with their texture when importing them into either Blender or MeshLab. Any suggestion how to take these rendering and successfully utilizing them into Blender? Thanks — SteveK, Jun 16 '17 at 10:42
@SteveK Hi, if you have question please ask on instead of posting answers. But before you proceed, please prepare a minimal example and explanation of what exactly is the problem. — Kuba, Jun 16 '17 at 11:28

score 9 · Answer 1 · answered Feb 11 '17 at 10:05

9

Don't rasterize. I think Texture is doing its own rasterization, so you are seeing the results of a double rasterization.

img = 
   Texture[
     Graphics[
       Table[Disk[{j, i}, Sqrt[i]/6], {i, 25}, {j, 50}], 
       PlotRange -> {{1, 50}, {-5, 25}}, ImageSize -> 600]];
SphericalPlot3D[1, {u, 0, Pi}, {v, 0, 2 Pi}, 
  Mesh -> None, 
  TextureCoordinateFunction -> ({#5, #4} &), 
  PlotStyle -> img, 
  Lighting -> {{"Ambient", White}}]

answered Feb 11 '17 at 10:05

m_goldberg

107,779
16
103
257

3

Well, this result seems satisfying enough, Thanks! But I would like to ask in advance, What if I only have the high quality rasterized image but not its original form? That rasterized image surely is clear enough for a very high quality texture but Mathematica returns a poor quality result. – Wjx Feb 11 '17 at 12:06
@Wjx. I don't know the answer to the question you raise in your comment. I have never been in the situation you describe. Perhaps someone else, who has, will chime in. – m_goldberg Feb 11 '17 at 14:29
Thanks for your contribution! I really really want to accept both if I could. but Wizard's solution is closer to what I want in mind, so I chose his. Thanks again! – Wjx Feb 12 '17 at 03:13

score 9 · Accepted Answer · edited Apr 13 '17 at 12:55

m_goldberg's solution jogged my memory and the problem is even a pitfall:

Use Rasterize[..., "Image"] to avoid double rasterization

Note that Rasterize[Grapphics[. . .]] is not an Image:

gr2d = Graphics[Table[Disk[{j, i}, Sqrt[i]/6], {i, 25}, {j, 50}], 
   PlotRange -> {{1, 50}, {-5, 25}}, ImageSize -> 1000];

Rasterize[gr2d] // Head

Graphics

Alexey's solution applied:

tex1 = Rasterize[gr2d, "Image"] // Texture;

SphericalPlot3D[1, {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> None, 
 TextureCoordinateFunction -> ({#5, #4} &), PlotStyle -> tex1, 
 Lighting -> {{"Ambient", White}}]

But I would like to ask in advance, What if I only have the high quality rasterized image but not its original form? That rasterized image surely is clear enough for a very high quality texture but Mathematica returns a poor quality result.

This is not a problem, in fact it is the solution, if you have an actual Image rather than a Raster.

img = gr2d // Image;

tex2 = Texture[img];

SphericalPlot3D[1, {u, 0, Pi}, {v, 0, 2 Pi}, Mesh -> None, 
 TextureCoordinateFunction -> ({#5, #4} &), PlotStyle -> tex2, 
 Lighting -> {{"Ambient", White}}]

Well, it seems this is a proper solution I want…… I've never thought I STILL will drop into pitfalls after so many years of fuzzing with Mathematica :( Thanks a lot! — Wjx, Feb 12 '17 at 03:02
@Wjx well I've been at it for ~17 years and I still couldn't give you a quick answer, so don't feel bad. Or laugh at me, whichever you prefer. — Mr.Wizard, Feb 12 '17 at 03:13

Degradation of image when used as texture in 3D graphics

2 Answers2