Applying non-Affine transforms to 2D polygons with textures

Question

I am trying to create a vanishing point perspective transformation of 2D polygons, for example transforming the red polygon into the blue polygon:

p1 = Polygon[{{0, 0}, {1, 0}, {1, 1}, {0, 1}}];
p2 = Polygon[{{0, 0}, {1, 0}, {0.55, 0.5}, {0.45, 0.5}}];
Graphics[{FaceForm[None], EdgeForm[Red], p1, EdgeForm[Blue], p2}]

Mathematica graphics

I can find the transformation easily enough with {err, tr} = FindGeometricTransform[First@p2, First@p1]; however, since the transformation is not an affine mapping, it cannot be handled by GeometricTransformation. Instead, I need to transform the points that make up the polygon:

Graphics[{FaceForm[None], EdgeForm[Red], p1, EdgeForm[Blue], Polygon@tr@First@p1}]

All seems well. If I try to apply a texture to the transformed polygon, things get ugly:

vop = VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}};
Graphics[{Texture[ExampleData[{"Texture", "Bricks3"}]], EdgeForm[Red],
  Polygon[tr@First@p1, vop]}]

Mathematica graphics

It appears that the internals of Texture can't handle the non-affine mapping very well, despite being able to handle affine transforms:

str = ShearingTransform[30 Degree, {1, 0}, {0, 1}]
Graphics[{Texture[ExampleData[{"Texture", "Bricks3"}]], EdgeForm[Red],
   Polygon[str@First@p1, vop]}]

Mathematica graphics

A rather clunky way around this problem is to use ImagePerspectiveTransformation, which was mentioned previously as having the ability to map any type of transform (affine or not).

ipt = ImagePerspectiveTransformation[
  ExampleData[{"Texture", "Bricks3"}], tr, Padding -> None]
Show[ipt, 
 Graphics[{FaceForm[None], EdgeForm[{Thick, Red}], 
   Polygon[First@ImageDimensions[ipt]*p2[[1]]]}], ImageSize -> 400]

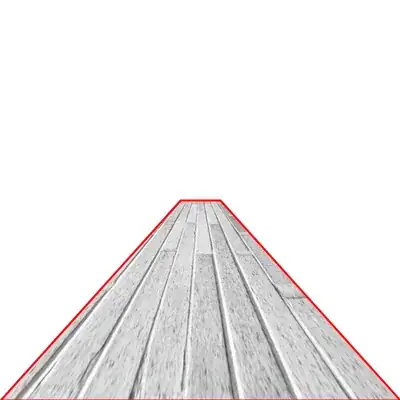
Mathematica graphics

This problem (I think) boils down to performing a non-affine transform to a texture, so I am wondering how (or if) this might be done efficiently than to perform the ImagePerspectiveTransformation on the texture image first?

You've probably considered it, but just for completeness: you can use ipt as a texture if you also apply the transformation to the texture coordinates: Graphics[{Texture[ipt], EdgeForm[Directive[Red, Thick]], Append[p2, VertexTextureCoordinates -> tr[p1[[1]]]]}] — J. M.'s missing motivation, Jun 01 '16 at 15:06

Silvia · Accepted Answer · 2014-03-27T19:58:34.723

I think the "ugly thing" might be because texture is interpolated on triangles (demonstrated after), and a quadrangle is only divided into 2 triangles - up-left and down-right. So to solve the problem, we just need a triangulation network with much higher resolution. One way is to use ParametricPlot:

ParametricPlot[
               Evaluate[tr@{u, v}], {u, 0, 1}, {v, 0, 1},
               PlotRange -> All, Mesh -> False, Axes -> False, Frame -> False,
               PlotStyle -> {Opacity[1], Texture[ExampleData[{"Texture", "Bricks3"}]]},
               TextureCoordinateFunction -> Function[{x, y, u, v}, {u, v}]
              ] //
Show[{Graphics[{FaceForm[None], EdgeForm[Red], p1,
                EdgeForm[{Blue, AbsoluteThickness[4]}], p2}],
      # }]&

vanishing point perspective transformation

Edit:

To demonstrate that texture is interpolated on triangles, we map a regular grid:

txtr = Plot[I, {x, 0, 1},
            PlotRange -> 10 {{-1, 1}, {-1, 1}},
            GridLines -> {
                          {#, Darker[Green]} & /@ Range[-10, 10],
                          {#, GrayLevel[.8]} & /@ Range[-10, 10]
                         },
            AspectRatio -> 1, Frame -> True, FrameStyle -> Directive[Red, Thick],
            AxesStyle -> Directive[Blue, Thick],
            FrameTicks -> {
                           {Range[-10, 10], False},
                           {{#, Style[#, Black]} & /@ Range[-10, 10], False}
                          }
           ]

regular grid

onto a pentagon:

Graphics[GraphicsComplex[{{0, 0}, {1, 0}, {1, 1}, {1/2, 1}, {0, 1}},
             {Texture[txtr], EdgeForm[Black],
              Polygon[Range[5],
                      VertexTextureCoordinates -> {{0, 0}, {1, 0},
                                                   {1.5, 1.3}, {.5, 1.2}, {-.7, 2}}
                     ],
              AbsolutePointSize[10], Point[Range[5]]
             }
        ]]

distorted texture

So we can see clearly, the pentagon is divided into 3 triangles.

Very nice - do you have a reference for interpolation of textures being done on triangles? — bobthechemist, Mar 27 '14 at 19:34
For those of us who are super picky, setting BoundaryStyle-> None in ParametricPlot removes the border that shows up in this function (but is obscured by p2 in the answer). — bobthechemist, Mar 28 '14 at 14:23

score 4 · Answer 2 · answered Mar 27 '14 at 16:45

You can use something designed for creating such ilusion :)

pic = Import["ExampleData/lena.tif"];
Manipulate[
 Graphics3D[{Texture@pic, Polygon[{{0, 0, 0}, {0, 1, 0}, {1, 1, 0}, {1, 0, 0}}, 
                          VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 1}, {0, 1}}]}, 
  ViewVertical -> {0, 0, 1}, ViewVector -> {{-.2, .5, h}, {100, .5, 0}}, 
  ViewAngle -> vAngle Degree, ImageSize -> {400, 400}],
 {{vAngle, 150}, 10, 179, 1},
 {{h, .7}, 0, 2}]

enter image description here

This is kind of joke answer and I will probably delete it later :) But worth to show I think.

I agree. There are a number of possibilities here, and depending on the project, manipulating View* may be the way to go. Constructive examples of manipulating the Graphics3D view I think are welcome and needed. — bobthechemist, Mar 27 '14 at 16:48

Applying non-Affine transforms to 2D polygons with textures

2 Answers2

Edit:

Linked