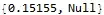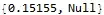Count the times a digit has appeared in a list as I scan the list

Question

Suppose I have a list l:

SeedRandom[1]
l = RandomInteger[5, 10]

{4, 2, 4, 0, 1, 0, 0, 2, 0, 0}

I want to count the times a certain digit has appeared in the list as I scan the list from left to right. I'd like the output to have the for $\color{red}{\text{\{digit, counts\}}}$ for every element.

This is my current method:

FoldPairList[{{#2, Count[#1, #2] + 1}, Append[#1, #2]}&, {}, l]

{{4, 1}, {2, 1}, {4, 2}, {0, 1}, {1, 1}, {0, 2}, {0, 3}, {2, 2}, {0, 4}, {0, 5}}

Any other elegant and mainstream method that can do this?

Answer 1

cnts = Transpose[{#, Module[{o = Ordering@#}, 
                      o[[o]] = Join @@ Range@Tally[#[[o]]][[All, 2]]; o]}] &;

Use (l containing desired list target):

result=cnts@l;

Will be order(s) of magnitude faster on large lists than OP method.

Answer 2

Here is a semi-imperative method:

runningCount[list_] := Module[{c}, c[_] = 0; {#, ++c[#]} & /@ list]

Example:

runningCount[{4, 2, 4, 0, 1, 0, 0, 2, 0, 0}]

(* {{4, 1}, {2, 1}, {4, 2}, {0, 1}, {1, 1}, {0, 2}, {0, 3}, {2, 2}, {0, 4}, {0, 5}} *)

Answer 3

I'll join the party :)

Clear["Global`*"]
lst = {4, 2, 4, 0, 1, 0, 0, 2, 0, 0}; 
Scan[(x[#] = 0) &, Union[lst]]; 
(Last@Reap@Scan[ Sow[{#, ++x[#]} ] &, lst])[[1]]

The idea is to set up a hash lookup counter of each number in the list, initially at zero. Then scan the list, incrementing the counter by one using lookup each time.

Timings

I did basic timings for the solutions given. all are using this list, and using AbsoluteTiming command

 lst = RandomInteger[10000, 50000];

Result

Ciao solution: 0.015831 seconds  
W Reach solution: 0.15155 seconds
Nasser solution: 0.22417 seconds
David Keith solution: 2.3196  seconds
A.G. solution:  145.95 seconds 

Code

Clear["Global`*"]
SeedRandom[1]
lst = RandomInteger[10000, 50000];
AbsoluteTiming[
 Scan[(x[#] = 0) &, Union[lst]];
 (Last@Reap@Scan[Sow[{#, ++x[#]}] &, lst])[[1]];
 ]

Clear["Global`*"]
SeedRandom[1]
lst = RandomInteger[10000, 50000];
AbsoluteTiming[
 Table[First@Tally@Reverse@Take[lst, i], {i, 1, Length@lst}];]

Clear["Global`*"]
SeedRandom[1]
lst = RandomInteger[10000, 50000];
counts[l_] := 
 Table[{l[[n]], Count[l[[1 ;; n]], l[[n]]]}, {n, Length[l]}]
AbsoluteTiming[counts[lst];]

Clear["Global`*"]
SeedRandom[1]
lst = RandomInteger[10000, 50000];
cnts = Transpose[{#, 
     Module[{o = Ordering@#}, 
      o[[o]] = Join @@ Range@Tally[#[[o]]][[All, 2]]; o]}] &;
AbsoluteTiming[cnts@lst;]

Clear["Global`*"]
SeedRandom[1]
lst = RandomInteger[10000, 50000];
runningCount[list_] := Module[{c}, c[_] = 0; {#, c[#] += 1} & /@ list]
AbsoluteTiming[runningCount[lst];]

Answer 4

Elegant :^)

Table[First@Tally@Reverse@Take[l, i], {i, 1, Length@l}]
{{4, 1}, {2, 1}, {4, 2}, {0, 1}, {1, 1}, {0, 2}, {0, 3}, {2, 2}, {0, 4}, {0, 5}}

(note that Tally lists distinct elements in the order they appear in l, thus the Reverse).

This is not however an efficient way to proceed for long lists, say $n\geq1000$. Time-complexity appears to be $O(n^2)$ while clearly a linear-time solution is feasible. Here are the running times for lists of size $n$ (random integers are in the $0-500$ range).

Times are on a 2015 Macbook Pro.

Answer 5

Compiling is usually the best approach for problems like this where an iteration depends on previous state. Here is a compiled function to get the counts (basically a compiled version of the approaches of @Nasser and @WReach)

iCount = Compile[{{d,_Integer,1}},
    Module[{z = ConstantArray[0, Max[d]-Min[d]+1]},
        Table[ ++z[[i]], {i, d-Min[d]+1}]
    ],
    CompilationTarget->"C"
];

iCount only produces the counts. Creating the actual desired output inside the compiled function was actually slower than using uncompiled code. So, here is the final function:

runningCount = Transpose @ Developer`ToPackedArray[{#, iCount[#]}]&;

Example (I compare with @ciao's function, since it is the fastest of the earlier methods):

data = RandomInteger[10000, 10^6];
r1 = runningCount[data]; //RepeatedTiming
r2 = cnts[data]; //RepeatedTiming
r1 === r2

{0.026, Null}

{0.17, Null}

True

Answer 6

Use Table:

l = {4, 2, 4, 0, 1, 0, 0, 2, 0, 0};

counts[l_] := 
 Table[{l[[n]], Count[l[[1 ;; n]], l[[n]]]}, {n, Length[l]}]

counts[l]

{{4, 1}, {2, 1}, {4, 2}, {0, 1}, {1, 1}, {0, 2}, {0, 3}, {2, 2}, {0, 4}, {0, 5}}

Answer 7

Catenate[KeyValueMap[Thread[{#, Range[Length[#2]]}] &,
  #]][[Ordering[Catenate[Values[#]]]]] &[PositionIndex[l]]

{{4, 1}, {2, 1}, {4, 2}, {0, 1}, {1, 1}, {0, 2}, {0, 3}, {2, 2}, {0, 4}, {0, 5}}