I want to resolve a PDE model, which is 1D heat diffusion equation with Neumann boundary conditions. The key problem is that I have some trouble in solving the equation numerically. Consider the following code:
h = 6000;
a = 200;
Dif = 3.67*10^-14*10^18;
Ni = 1;
deq = D[u[t, x], t] == Dif*D[u[t, x], {x, 2}]
ic = u[0, x] == If[0 <= x <= a , Ni, 0]
bc = {Derivative[0, 1][u][t, 0] == 0, Derivative[0, 1][u][t, h] == 0}
sol = NDSolve[{deq, ic, bc}, u, {t, 0, 60}, {x, 0, h}]
Plot3D[Evaluate[u[t, x] /. sol], {t, 0, 60}, {x, 0, h}, PlotStyle -> Automatic]
I got a result, but a error was occurred.
NDSolve::ibcinc:
I know that this error suggests conflicts between initial condition and boundary conditions, although I have no idea where conflict come from.
In addition, as you can see, the value of x=0 is gradually increased with time in spite of Neumann conditions.
Any suggestions how to fix it?
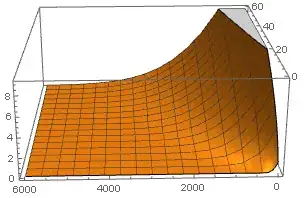
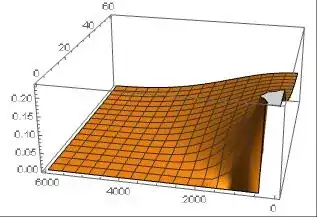
Method -> {"MethodOfLines", "DifferentiateBoundaryConditions" -> {True, "ScaleFactor" -> 100}, "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> 1000, "MinPoints" -> 1000, "DifferenceOrder" -> 4}}toNDSolvewill resolve your problem. – xzczd Mar 04 '17 at 17:48