Finding intersection of two ellipses

Question

I am trying to find the intersection points of two ellipses, given in a parametric form:

a = 1;
e = 0.7;
ϕ = π/6;
rotv = Normalize@{1, -1, 0};
x[θ_] := -a*e + a*Cos[θ];
y[θ_] := a Sqrt[1 - e^2]*Sin[θ];
rot = RotationMatrix[ϕ, rotv];
Solve[{x[θ1], y[θ1], 0} == 
  rot.{x[θ2], y[θ2], 0}, {θ1, θ2}]

But with this I get an empty output {}. But if I do:

el1[θ_] = {x[θ], y[θ], 0};
el2[θ_] = rot.{x[θ], y[θ], 0};
Solve[el2[t][[3]] == 0, t]
(*{{t -> -0.344559}, {t -> 1.58487}}*)

and

el1[-0.3445591705449694`]
el2[-0.3445591705449694`]

(*{0.241224, -0.241224, 0}*)
(*{0.241224, -0.241224, 0.}*)

so the solution exists but I wonder why, the above approach does not yield a result? (there is a similar question here but I do not really understand it much, I am basing my attempt on this)

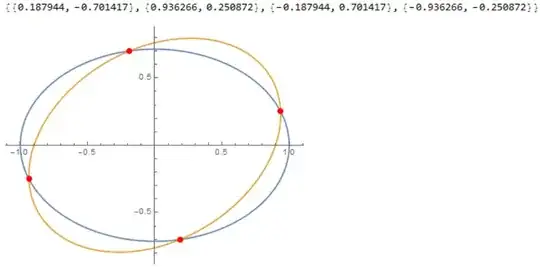
Is there a reason you're solving a multivariate version in Solve? I don't think it's necessary. And by using the univariate form (what you more or less do in your second case) and by restricting the domain of the solutions (since it's parametrized and you only need one full orbit) you can get it to work. Alternatively you can remove the values for the coefficients and it will spit out the exact answer. — b3m2a1, Mar 08 '17 at 20:44
Since you are only looking for a numerical solution, I would use NMinimize: NMinimize[ Norm[{x[\[Theta]1], y[\[Theta]1], 0} - rot.{x[\[Theta]2], y[\[Theta]2], 0}], {\[Theta]1, \[Theta]2}] — bill s, Mar 08 '17 at 20:47
@MB1965 Not really, I am happy with the univariate solution. But regardless of this, I am interested, what I am doing wrong or why the multivariate approach seems to fail (specifically if I take into account that a similar example is used on Wolfram's site) — atapaka, Mar 08 '17 at 20:52
@leosenko that example is fundamentally different from yours. Yours is a parametric description so their x and y are combined into your \[Theta]. What would have been your r is assumed to be 1 which theirs is forced to be by a domain restriction to Circle[{0,0},1]. Second, you need a domain restriction of some form. Using the exact form forces it to be restricted because the solutions involve Arc*, which have restriction built into the definition. Otherwise (for the numerical version) you need to supply one yourself. — b3m2a1, Mar 08 '17 at 20:56
@LouisB Wow. I'm impressed Mathematica's clever enough to take the infinite set of solutions and properly convert it to a ConditionalExpression. You should provide that plus a little bit of explanation for how it affects Solve as a proper answer. — b3m2a1, Mar 08 '17 at 21:33
your first approach is three equations in two unknowns. There is a solution in this case but Solve will fail if it needs to resort to numerical methods. A better approach to this is to note the solution is where the rotation vector intersects the first ellipse, so Solve[{x[t], y[t]} == c rotv[[1 ;; 2]] , {c, t}] (Which will work with inexact parameters ) — george2079, Mar 08 '17 at 22:01
I think it should be possible to do this using geometric regions and RegionIntersection. — masterxilo, Mar 09 '17 at 22:22

score 4 · Answer 1 · answered Mar 09 '17 at 07:35

a = 1;
e = 0.7;
b = x /. Quiet[Solve[Sqrt[1 - x^2/a^2] == e && x > 0, x][[1]]];
ro = RotationMatrix[Pi/6];
ell1[t_] := {a Cos[t], b Sin[t]}
ell2[t_] := ro.ell1[t]
int = ell1[t] /. Quiet[Solve[ell1[t] == ell2[s], {s, t}]]
ParametricPlot[{ell1[t], ell2[t]}, {t, 0, 2 Pi}, 
 Epilog -> {Red, PointSize[0.02], Point[int]}]

Finding intersection of two ellipses

1 Answers1