Different Boundary Style on each edge of 3D Plot

Question

I am wondering is there a possibility to define different properties on each edge of Plot3D (different colours or thicknesses) by using BoundaryStyle?

Answer 1

Update 2: We can avoid manual adjustments in the mesh specifications for mesh lines on the boundary using the option Method -> {"BoundaryOffset" -> False} (see this answer by MichaelE2):

 Plot3D[Sin[x + y^2], {x, -3, 3}, {y, -3, 3},
  BoundaryStyle -> None, 
  PlotStyle -> Opacity[.7], 
  MeshFunctions -> {# &, #2 &}, 
  Mesh -> {{{-3, Directive[Thick, Red]}, {3, Directive[Thick, Cyan]}}, 
      {{-3, Directive[Thick, Purple]}, {3, Directive[Thick, Blue]}}}, 
  Method -> {"BoundaryOffset" -> False}]

Update: an alternative approach using ParametricPlot3D:

ClearAll[boundaryPlot3D]
boundaryPlot3D[func : _[__], a : {x_, x1_, x2_}, b : {y_, y1_, y2_}, 
   pltstyle_: {Red, Orange, Blue, Purple}][o : OptionsPattern[]] := 
 Module[{fs = (({x, y, func} /. #) & /@ ((Thread[# -> {##2}] & @@ #)) /. 
        y | x -> u ) & /@ {a, b}, styles = Partition[pltstyle, 2]}, 
  Show[ParametricPlot3D[{x, y, func}, a, b, o, Mesh -> None, 
    PlotStyle -> Opacity[.5]], 
   ParametricPlot3D[Evaluate@fs[[1]], {u, y1, y2}, 
    PlotStyle -> styles[[1]], o, BaseStyle -> Thick],
   ParametricPlot3D[Evaluate@fs[[2]], {u, x1, x2}, 
    PlotStyle -> styles[[2]], o, BaseStyle -> Thick], 
   PlotRange -> All]]

Examples:

boundaryPlot3D[Sin[x + y^2], {x, -3, 3}, {y, -3, 3}][]

boundaryPlot3D[Sin[x + y^2], {x, -6, 6}, {y, -3, 3}][]

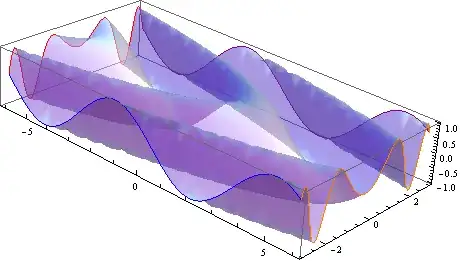
boundaryPlot3D[
  Sin[x y + y^2], {x, -3, 3}, {y, -6, 6}, {Directive[Thick, Red], 
   Directive[Thick, Dashed, Green], Directive[Thick, Dashed, Orange], Purple}][]

boundaryPlot3D[Sin[x + x y + y^2], {x, -3, 3}, {y, -3, 3}][] /. 
 Line -> (Tube[#, .1] &)

Original answer:

I don't think it can be done using BoundaryStyle, but you can use MeshFunctions and Mesh to get the desired result:

Plot3D[Sin[x + y^2], {x, -3, 3}, {y, -3, 3}, BoundaryStyle -> None, 
 PlotStyle -> Opacity[.7],  MeshFunctions -> {# &, #2 &}, 
 Mesh -> {{{-3 + .001, Directive[Thick, Red]}, 
           {3 - .001,  Directive[Thick, Orange]}}, 
          {{-3 + .001, Directive[Thick, Purple]}, 
           {3 - .001, Directive[Thick, Blue]}}}]

Plot3D[Sin[x + y^2], {x, -6, 6}, {y, -3, 3}, BoundaryStyle -> None, 
 PlotStyle -> Opacity[.5], MeshFunctions -> {# &, #2 &}, 
 Mesh -> {{{-6 + .001, Directive[Thick, Red]}, 
           {6 - .001,  Directive[Thick, Orange]}},
          {{-3 + .001, Directive[Thick, Purple]}, 
           {3 - .001, Directive[Thick, Blue]}}}]