Draw a triangulated sphere

Question

How to draw a triangulated sphere such as the one below in Mathematica, without being restricted to these colors, but with a more uniform color (possibly with some shaded area), and with the background frame removed?

Which version are you in? You can get this type of deal using the region functionality pretty easily. — b3m2a1, Mar 31 '17 at 04:27
Use Geodesate[] from the Polyhedron Operations package (Needs["PolyhedronOperations`"]), or use the region discretization functionality on a Sphere[]. — J. M.'s missing motivation, Mar 31 '17 at 04:36
@J.M. Problem with RegionDiscretize is the coloring. It's a bit of a pain to color each cell, last I remembered. I'm currently trying it with Lighting. — b3m2a1, Mar 31 '17 at 04:37

score 7 · Answer 1 · edited Apr 13 '17 at 12:55

7

Perhaps,

r = DiscretizeRegion[Sphere[]];
pg = MeshPrimitives[r, 2];
Graphics3D[
 pg /. Polygon[
    u___] :> {ColorData["Rainbow"][
     Rescale[Max[u[[All, 3]]], {-1, 1}]], Polygon[u]}, Axes -> True]

:

Exploiting this answer

Manipulate[
 r = BoundaryDiscretizeRegion[Ball[], 
   MaxCellMeasure -> {"Length" -> lg}, PrecisionGoal -> 0.01];
 pg = MeshPrimitives[r, 2];
 Graphics3D[
  pg /. Polygon[
     u___] :> {ColorData["Rainbow"][
      Rescale[Max[u[[All, 3]]], {-1, 1}]], Polygon[u]}, 
  Axes -> True], {lg, {0.1, 0.5, 1, 3}}]

edited Apr 13 '17 at 12:55

Community

1

answered Mar 31 '17 at 04:48

ubpdqn

60,617
3
59
148

@ubpdqn Ahh. Of course. Going straight to the Graphics3D is much better. – b3m2a1 Mar 31 '17 at 04:51

score 5 · Accepted Answer · edited Jun 16 '20 at 09:23

5

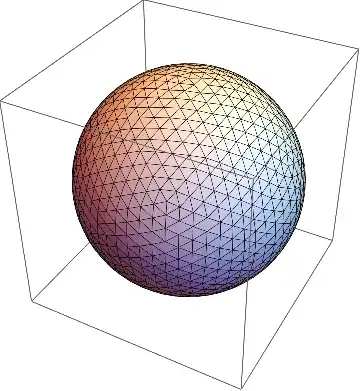
If you're a) on 10+ and b) don't need this cells to truly be colored, you can try this:

mesh = DiscretizeRegion@Sphere[];
MeshRegion[mesh,
 Lighting -> Sequence @@@ {
    ConstantArray[{"Point", Red, {0, 0, 75}}, 2],
    Map[{"Point", Yellow, Append[#, 0]} &,
     CirclePoints[3., 6]
     ],
    ConstantArray[{"Point", Blue, {0, 0, -75}}, 2]
    },
 MeshCellHighlight -> {{1, All} -> Black}
]

This is just tricking you into thinking it's colored using Lighting. I was too lazy to highlight each cell. It's possible to write code to color an arbitrary discretized surface at the cell level. I've done it, but it's more code than I want to post here and isn't thoroughly proof-read. If you need that I can dig it up from wherever it's hiding, though.

Update

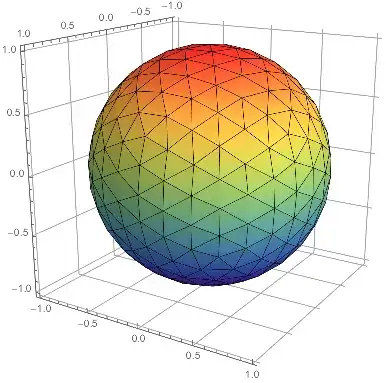
OP mentions in the comments that he's really interested in the triangulation. That's easily extracted as such:

triangulation =
  With[{cds = MeshCoordinates@mesh},
   MeshCells[mesh, 2] /. i_Integer :> cds[[i]]
   ];

And just to check that we pulled it out right:

triangulation // Graphics3D

edited Jun 16 '20 at 09:23

Community

1

answered Mar 31 '17 at 04:41

b3m2a1

46,870
3
92
239

Thanks, but I hope to have the "triangulated" grid for the math purpose. (Not for the art purpose.) – wonderich Mar 31 '17 at 04:44
@wonderich Then your life is much easier. Use MeshCoordinates. I'll post an addendum. – b3m2a1 Mar 31 '17 at 04:45
@wonderich Added. – b3m2a1 Mar 31 '17 at 04:49
+1 for Lighting.BTY,MeshCellHighlight -> {{1, All} -> Black} is more similar with OP – yode Mar 31 '17 at 04:49
@MB1965 thanks for lesson on Lighting +1 :) – ubpdqn Mar 31 '17 at 04:50
@yode Nice point. I included it. – b3m2a1 Mar 31 '17 at 04:53
Have you noted we cannot make that triangle be more lager when we discretize a sphere? – yode Mar 31 '17 at 05:11
And we can use MeshPrimitives[mesh, 2] – yode Mar 31 '17 at 05:15
@yode you can probably increase the mesh size in the discretize call. I just remembered about SliceDensityPlot3D which solves the OPs problem better. Unable to post it right now, though, so feel free to put it out there SliceDensityPlot3D[z, mesh, {x,-1,1}, {y,-1,1},{z,-1,1},ColorFunction->"Rainbow"] should do it. – b3m2a1 Mar 31 '17 at 05:26
Your SliceDensityPlot3D work well,just we cannot set the edge be Black. – yode Mar 31 '17 at 05:32
@yode use /._EdgeForm->EdgeForm[Black] – b3m2a1 Mar 31 '17 at 05:33
I post it as a answer here.And I have specified that is your work. :) – yode Mar 31 '17 at 05:38
Thanks again, I wonder whether there is a way to change the number of triangulation (to fewer triangles)? – wonderich Mar 31 '17 at 16:01
@wonderich Sure there is. You'd change it in the discretize call. See the various other answers for an example. In part two of yode's answer I tweaked things to basically exactly reproduce your picture. Did that by reducing how fine a mesh it triangulated. – b3m2a1 Mar 31 '17 at 16:03
In your first part answer, using "MeshRegion" -- what values should I adjust to change the number of triangulations? Thanks! – wonderich Mar 31 '17 at 16:11
@wonderich It's actually in the the call to DiscretizeRegion that you'll want to change things. Try mesh = DiscretizeRegion[Sphere[], MaxCellMeasure->{"Length" -> .35}, PrecisionGoal -> .01]. That's what I used here – b3m2a1 Mar 31 '17 at 16:14

score 4 · Answer 3 · edited Apr 13 '17 at 12:56

4

Method One

mesh = DiscretizeRegion@Sphere[];
Graphics3D[Transpose[{ColorData["Rainbow"] /@ 
    Rescale[Last /@ PropertyValue[{mesh, 2}, MeshCellCentroid]], 
   MeshPrimitives[mesh, 2]}]]

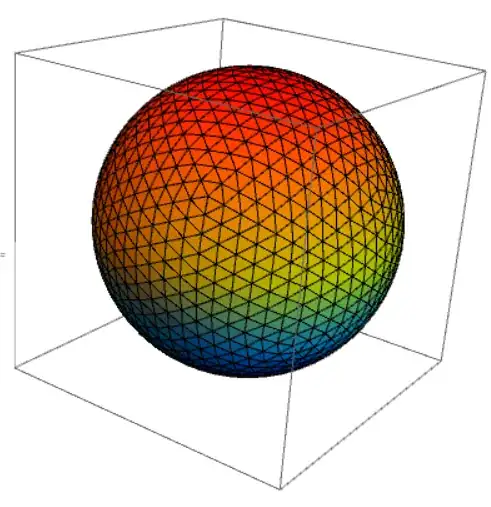
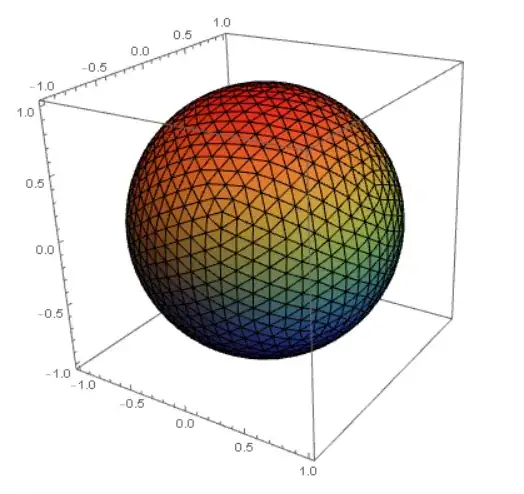
Method two(Based on this comment)

mesh = DiscretizeRegion[Sphere[]];
SliceDensityPlot3D[z, mesh, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, 
  ColorFunction -> "Rainbow"] /. _EdgeForm -> EdgeForm[Black]

MB1965 tweaks to Method two:

mesh = DiscretizeRegion[Sphere[],
   MaxCellMeasure -> {"Length" -> .35},
   PrecisionGoal -> .01];
SliceDensityPlot3D[z,
  mesh, {x, -1, 1}, {y, -1, 1}, {z, -1, 1},
  ColorFunction -> "Rainbow",
  FaceGrids ->
   -IdentityMatrix[3],
  AxesEdge -> {
    {-1, 1},
    {1, -1},
    {1, -1}
    },
  Boxed -> False
  ] /. _EdgeForm -> EdgeForm[Black]

edited Apr 13 '17 at 12:56

Community

1

answered Mar 31 '17 at 05:27

yode

26,686
4
62
167

@MB1965 Perfect.Sorry cannot upvote. :) – yode Mar 31 '17 at 07:32
I just realized we have three different ways Mathematica can do coloring on this page. This way here clearly uses layered textures, because there are gradients in the cells. The Lighting way does colors in the rendering system. And the way @ubpqdn did it colors individual faces. Pretty cool for such a simple question. – b3m2a1 Mar 31 '17 at 07:35

Draw a triangulated sphere

3 Answers3

Update

Method One

Method two(Based on this comment)

MB1965 tweaks to Method two:

Linked