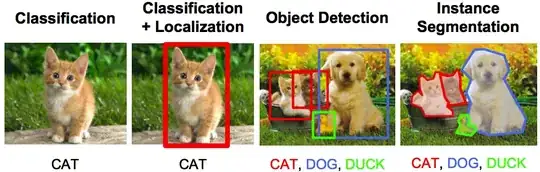
Introduction
An object detection problem can be approached as either a classification problem or a regression problem. As a classification problem, the image is divided into small patches, each of which will be run through a classifier to determine whether there are objects in the patch. Then the bounding boxes will be assigned to locate around patches that are classified with a high probability of present of an object. In the regression approach, the whole image will be run through a convolutional neural network to directly generate one or more bounding boxes for objects in the images.

In this answer, we will build an object detector using the tiny version of the You Only Look Once (YOLO) approach.
Construct the YOLO network
The tiny YOLO v1 consists of 9 convolution layers and 3 full connected layers. Each convolution layer consists of convolution, leaky relu and max pooling operations. The first 9 convolution layers can be understood as the feature extractor, whereas the last three full connected layers can be understood as the "regression head" that predicts the bounding boxes.
There is no native leaky relu layer in Mathematica, but it can be constructed easily using a ElementwiseLayer
leayReLU[alpha_] := ElementwiseLayer[Ramp[#] - alpha*Ramp[-#] &]
with this, the YOLO network can be constructed as
YOLO = NetInitialize@NetChain[{
ElementwiseLayer[2.*# - 1. &],
ConvolutionLayer[16, 3, "PaddingSize" -> 1],
leayReLU[0.1],
PoolingLayer[2, "Stride" -> 2],
ConvolutionLayer[32, 3, "PaddingSize" -> 1],
leayReLU[0.1],
PoolingLayer[2, "Stride" -> 2],
ConvolutionLayer[64, 3, "PaddingSize" -> 1],
leayReLU[0.1],
PoolingLayer[2, "Stride" -> 2],
ConvolutionLayer[128, 3, "PaddingSize" -> 1],
leayReLU[0.1],
PoolingLayer[2, "Stride" -> 2],
ConvolutionLayer[256, 3, "PaddingSize" -> 1],
leayReLU[0.1],
PoolingLayer[2, "Stride" -> 2],
ConvolutionLayer[512, 3, "PaddingSize" -> 1],
leayReLU[0.1],
PoolingLayer[2, "Stride" -> 2],
ConvolutionLayer[1024, 3, "PaddingSize" -> 1],
leayReLU[0.1],
ConvolutionLayer[1024, 3, "PaddingSize" -> 1],
leayReLU[0.1],
ConvolutionLayer[1024, 3, "PaddingSize" -> 1],
leayReLU[0.1],
FlattenLayer[],
LinearLayer[256],
LinearLayer[4096],
leayReLU[0.1],
LinearLayer[1470]
},
"Input" -> NetEncoder[{"Image", {448, 448}}]
]

Load pre-trained weights
Training the YOLO network is time-consuming. We will use the pre-trained weights instead. The pre-trained weights can be downloaded as a binary file from here (172M).
Using NetExtract and NetReplacePart we can load the pre-trained weights into our model
modelWeights[net_, data_] :=
Module[{newnet, as, weightPos, rule, layerIndex, linearIndex},
layerIndex =
Flatten[Position[
NetExtract[net, All], _ConvolutionLayer | _LinearLayer]];
linearIndex =
Flatten[Position[NetExtract[net, All], _LinearLayer]];
as = Flatten[
Table[{{n, "Biases"} ->
Dimensions@NetExtract[net, {n, "Biases"}], {n, "Weights"} ->
Dimensions@NetExtract[net, {n, "Weights"}]}, {n, layerIndex}],
1];
weightPos = # + {1, 0} & /@
Partition[Prepend[Accumulate[Times @@@ as[[All, 2]]], 0], 2, 1];
rule = Table[
as[[n, 1]] ->
ArrayReshape[Take[data, weightPos[[n]]], as[[n, 2]]], {n, 1,
Length@as}];
newnet = NetReplacePart[net, rule];
newnet = NetReplacePart[newnet,
Table[
{n, "Weights"} ->
Transpose@
ArrayReshape[NetExtract[newnet, {n, "Weights"}],
Reverse@Dimensions[NetExtract[newnet, {n, "Weights"}]]], {n,
linearIndex}]];
newnet
]
data = BinaryReadList["yolo-tiny.weights", "Real32"][[5 ;; -1]];
YOLO = modelWeights[YOLO, data];
Post-processing
The output of this network is a 1470 vector, which contains the coordinates and confidence of the predicted bounding boxes for different classes. The tiny YOLO v1 is trained on the PASCAL VOC dataset which has 20 classes:
labels = {"aeroplane", "bicycle", "bird", "boat", "bottle", "bus",
"car", "cat", "chair", "cow", "diningtable", "dog", "horse",
"motorbike", "person", "pottedplant", "sheep", "sofa", "train",
"tvmonitor"};
And the information for the output vector from the network is organized in the following way

The 1470 vector output is divided into three parts, giving the probability, confidence and box coordinates. Each of these three parts is also further divided into 49 small regions, corresponding to the predictions at each cell. Each of the 49 cells will have two box predictions. In postprocessing steps, we take this 1470 vector output from the network to generate the boxes that with a probability higher than a certain threshold. The overlapping boxes will be resolved using the non-max suppression method.
coordToBox[center_, boxCord_, scaling_: 1] := Module[{bx, by, w, h},
(*conver from {centerx,centery,width,height} to Rectangle object*)
bx = (center[[1]] + boxCord[[1]])/7.;
by = (center[[2]] + boxCord[[2]])/7.;
w = boxCord[[3]]*scaling;
h = boxCord[[4]]*scaling;
Rectangle[{bx - w/2, by - h/2}, {bx + w/2, by + h/2}]
]
nonMaxSuppression[boxes_, overlapThreshold_, confidThreshold_] :=
Module[{lth = Length@boxes, boxesSorted, boxi, boxj},
(*non-max suppresion to eliminate overlapping boxes*)
boxesSorted =
GroupBy[boxes, #class &][All, SortBy[#prob &] /* Reverse];
Do[
Do[
boxi = boxesSorted[[c, n]];
If[boxi["prob"] != 0,
Do[
boxj = boxesSorted[[c, m]];
(*if two boxes overlap largely,
kill the box with low confidence*)
If[RegionMeasure[
RegionIntersection[boxi["coord"], boxj["coord"]]]/
RegionMeasure[RegionUnion[boxi["coord"], boxj["coord"]]] >=
overlapThreshold,
boxesSorted = ReplacePart[boxesSorted, {c, m, "prob"} -> 0]];
, {m, n + 1, Length[boxesSorted[[c]]]}]
]
, {n, 1, Length[boxesSorted[[c]]]}],
{c, 1, Length@boxesSorted}
];
boxesSorted[All, Select[#prob > 0 &]]]
labelBox[class_ -> box_] := Module[{coord, textCoord},
(*convert class\[Rule]boxes to labeled boxes*)
coord = List @@ box;
textCoord = {(coord[[1, 1]] + coord[[2, 1]])/2.,
coord[[1, 2]] - 0.04};
{{GeometricTransformation[
Text[Style[labels[[class]], 30, Blue], textCoord],
ReflectionTransform[{0, 1}, textCoord]]},
EdgeForm[Directive[Red, Thick]], Transparent, box}
]
drawBoxes[img_, boxes_] := Module[{labeledBoxes},
(*draw boxes with labels*)
labeledBoxes =
labelBox /@
Flatten[Thread /@ Normal@Normal@boxes[All, All, "coord"]];
Graphics[
GeometricTransformation[{Raster[ImageData[img], {{0, 0}, {1, 1}}],
labeledBoxes}, ReflectionTransform[{0, 1}, {0, 1/2}]]]
]
postProcess[img_, vec_, boxScaling_: 0.7, confidentThreshold_: 0.15,
overlapThreshold_: 0.4] :=
Module[{grid, prob, confid, boxCoord, boxes, boxNonMax},
grid = Flatten[Table[{i, j}, {j, 0, 6}, {i, 0, 6}], 1];
prob = Partition[vec[[1 ;; 980]], 20];
confid = Partition[vec[[980 + 1 ;; 980 + 98]], 2];
boxCoord = ArrayReshape[vec[[980 + 98 + 1 ;; -1]], {49, 2, 4}];
boxes = Dataset@Select[Flatten@Table[
<|"coord" ->
coordToBox[grid[[i]], boxCoord[[i, b]], boxScaling],
"class" -> c,
"prob" -> If[# <= confidentThreshold, 0, #] &@(prob[[i, c]]*
confid[[i, b]])|>
, {c, 1, 20}, {b, 1, 2}, {i, 1, 49}
], #prob >= confidentThreshold &];
boxNonMax =
nonMaxSuppression[boxes, overlapThreshold, confidentThreshold];
drawBoxes[Image[img], boxNonMax]
]
Results
These are the results for this network.
urls = {"http://i.imgur.com/n2u0N3K.jpg",
"http://i.imgur.com/Bpb60U1.jpg", "http://i.imgur.com/CMZ6Qer.jpg",
"http://i.imgur.com/lnEE8C7.jpg"};
imgs = Import /@ urls

With[{i = ImageResize[#, {448, 448}]}, postProcess[i, YOLO[i]]] & /@
imgs // ImageCollage

Reference
- Vehicle detection using YOLO in Keras, https://github.com/xslittlegrass/CarND-Vehicle-Detection
- J. Redmon, S. Divvala, R. Girshick, and A. Farhadi, You Only Look Once: Unified, Real-Time Object Detection, arXiv:1506.02640 (2015).
- J. Redmon and A. Farhadi, YOLO9000: Better, Faster, Stronger, arXiv:1612.08242 (2016).
- darkflow, https://github.com/thtrieu/darkflow
- Darknet.keras, https://github.com/sunshineatnoon/Darknet.keras/
- YAD2K, https://github.com/allanzelener/YAD2K