ListLogPlot with negative errorbars

Question

So I have been reading Plotting Error Bars on a Log Scale on how to implement errorbars with a logarithmic y-scale but I have another problem: some of my errorbars are negative values and I don't know how to implement this in the graph.

I don't know if this is even possible but if anyone knows a solution I'd be very happy to hear it. Thanks in advance.

One reason for obtaining the lower end of the error bar being negative when you have positive data is that your distribution is skewed and using plus-or-minus one or two standard deviations (or standard errors) is a poor description of where the data is located (using standard deviations) or how well you've estimated the mean (using standard errors). What you really need to give is a complete example (code and data) if you want a solution targeted to your problem. — JimB, Apr 23 '17 at 21:26

score 0 · Accepted Answer · answered Apr 23 '17 at 19:32

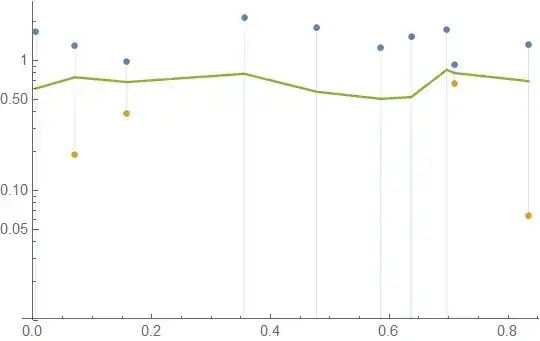
Non-positive numbers are not real, so they cannot be plotted on the log scale. If these numbers are actually non-physical, like negative absolute temperatures or expected life, you might reconsider how the error limits are being computed. If they are physical, but uninteresting, you could replace them with positive numbers smaller than the smallest interesting values, and then restrict the range of the plot to let them truncate. This might serve the purpose of displaying the data.

In the code below, the code by @Dr. Belisarius has been modified to accomplish this:

dataX=Sort@RandomReal[1,10];
dataY=RandomReal[{0.5,1},10];
error=RandomReal[1.5,10];
f[y_]:=Transpose[{dataX,y}];
plusMinus[a_,b_]:={a+b,a-b,a};
plusMinListRaw=Thread[plusMinus[dataY,error]];
(* smaller than smallest interesting value *)
minVal=0.001;
(* replace non-positive numbers with minVal *)
plusMinList={#[[1]],If[#[[2]]<=0,minVal,#[[2]]],#[[3]]}&/@plusMinListRaw;
(* restrict lower range using opts *)
ePlot[plotFun_,dataX_,plusMinList_,opts___]:=plotFun[{f[plusMinList[[All,1]]],f[plusMinList[[All,2]]],f[plusMinList[[All,3]]]},Filling->{1->{2}},Joined->{False,False,True},opts]
ePlot[ListLogPlot,dataX,plusMinList,PlotRange->{Automatic,{10 minVal,All}}]

This should be sufficient for what I want to do as the negative errorbars don't actually represent something physical so this does the job very well. Thanks a lot! — D haverkamp, Apr 24 '17 at 08:30

ListLogPlot with negative errorbars

1 Answers1