Plotting Error Bars on a Log Scale

Question

I have a plot with ErrorListPlot

data = Sort@RandomReal[1, {10, 2}];
error = RandomReal[0.5, 10];
errorplot = ErrorListPlot[
  Partition[Riffle[data, ErrorBar /@ error], 2],
  Joined -> True]

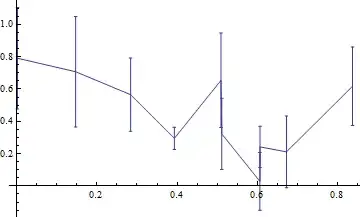
Mathematica graphics

However, I would like to have it with the y-axis on a log scale. I can use ListLogPlot to get the log scale but this doesn't plot the errorbars.

logplot = ListLogPlot[
  data,
  PlotRange -> All,
  AxesOrigin -> {0, 0},
  Joined -> True
  ]

Mathematica graphics

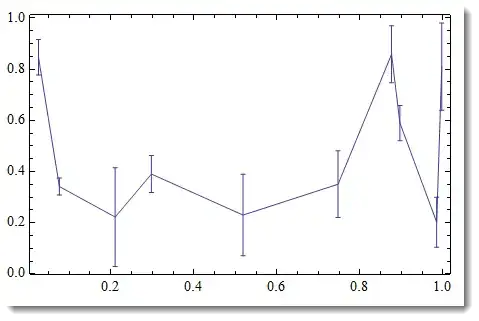
I tried Show[logplot, errorplot, PlotRange->All] to see if it would plot with the scale and ticks from the logplot but that didn't work right:

Mathematica graphics

I also tried to take the Ticks from the logplot: Show[errorplot, Ticks -> Ticks /. AbsoluteOptions@logplot] but that just gives an error.

I tried to manually take the log of the data and then grab the tick-marks but that didn't work right

data = Sort@RandomReal[{10, 100}, {10, 2}];
error = RandomReal[20, 10];
logdata = Transpose[{data[[All, 1]], Log[10, data[[All, 2]]]}];
errorup = Log[10, data[[All, 2]] + error] - logdata[[All, 2]];
errordown = Log[10, data[[All, 2]] - error] - logdata[[All, 2]];
logerror = Log[10, error];
logplot = ListLogPlot[
  data,
  Joined -> True,
  AxesOrigin -> {0, 0}
  ]
errorlogplot = ErrorListPlot[
  Partition[
   Riffle[logdata, ErrorBar /@ Transpose[{errordown, errorup}]], 2],
  Joined -> True,
  AxesOrigin -> {0, 0}
  ]
errorlogplot2 = ErrorListPlot[
  Partition[
   Riffle[logdata, ErrorBar /@ Transpose[{errordown, errorup}]], 2],
  Joined -> True,
  AxesOrigin -> {0, 0},
  Ticks -> (Ticks /. AbsoluteOptions@logplot)
  ]

Mathematica graphics

Is there an easy way to do this?

On the log scale the error bars will appear asymmetrical.

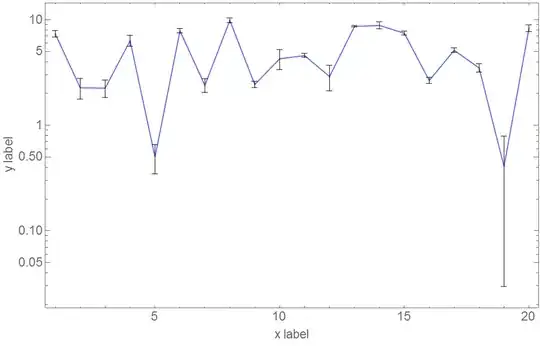
Have you tried LevelScheme? It's CustomTicks package is a superior alternative to trying to set it up by hand. The edition I have installed isn't functioning correctly, otherwise I would have posted it as an answer. But, it is worth a look. — rcollyer, Apr 04 '12 at 03:58
Do you realize that 2 of your error bars on 1st plot have negative y-values? I guess it is an accident of making up a random data set, yet we should be aware of these logs of negative values. — Vitaliy Kaurov, Apr 04 '12 at 07:53
@Vitaliy Kaurov, I realized that after I played with my random data more. I was originally working with a real dataset but it was simpler to post a line to generate random data then upload and link to the real data, however, my random data was slightly broken as you noticed. — s0rce, Apr 04 '12 at 19:30

Dr. belisarius · Answer 1 · 2012-04-04T16:08:55.350

30

Without using the "ErrorBarPlots`" Package

dataX = Sort@RandomReal[1, 10];
dataY = RandomReal[{0.5, 1}, 10];
error = RandomReal[0.5, 10];
errorH = dataY + error;
errorL = dataY - error;
f[y_] := Transpose[{dataX, y}];

ListLogPlot[{f[errorH], f[errorL], f[dataY]}, 
            Filling -> {1 -> {2}}, 
            Joined -> {False, False, True}]

enter image description here

Edit

Following @rcollyer's suggestion

dataX = Sort@RandomReal[1, 10];
dataY = RandomReal[{0.5, 1}, 10];
error = RandomReal[0.5, 10];
f[y_] := Transpose[{dataX, y}];

PlusMinus[a_, b_] := {a + b, a - b, a};
plusMinList = Thread[PlusMinus[dataY, error]];

ePlot[plotFun_, dataX_, plusMinList_] :=
 plotFun[{
   f[plusMinList[[All, 1]]],
   f[plusMinList[[All, 2]]],
   f[plusMinList[[All, 3]]]},
  Filling -> {1 -> {2}},
  Joined -> {False, False, True}]
ePlot[ListLogPlot, dataX, plusMinList]

edited Apr 04 '12 at 16:08

answered Apr 04 '12 at 14:50

Dr. belisarius

115,881
13
203
453

1

@rcollyer Thanks! Filling is widely supported by almost all Plotting primitives. I use it always to draw error bars. – Dr. belisarius Apr 04 '12 at 14:59
This could easily be transformed into a function that accepts the form {_, PlusMinus[_,_} and plots it on the plotting function of your choice: ListPlot, ListLogPlot, etc. – rcollyer Apr 04 '12 at 15:05
@rcollyer Done :) – Dr. belisarius Apr 04 '12 at 15:57
I'd put PlusMinus inside of a Block to prevent corrupting Global`, and accept d:{{_, PlusMinus[_,_]}..}. – rcollyer Apr 04 '12 at 16:37
4

Nice! If more traditional error bars are desirable, options can be added: ListLogPlot[..., PlotMarkers -> {"-", "-", "\[FilledCircle]"}] – Vitaliy Kaurov Apr 04 '12 at 17:34
Thanks very much. I used your filling idea to create continuous filled error bounds: http://i.stack.imgur.com/wPvOR.png – s0rce Apr 04 '12 at 20:34
@s0rce Nice plot! – Dr. belisarius Apr 04 '12 at 21:01
@R.M Thanks! As a matter of fact I answered a more difficult one here http://stackoverflow.com/a/8032684/353410 – Dr. belisarius Apr 05 '12 at 21:31
Nice, but how can I draw horizontal error bars? – Frank Breitling Mar 22 '17 at 12:07

Vitaliy Kaurov · Answer 2 · 2012-04-04T07:32:17.830

A one-liner solution (see a bit below lengthy explanation)

This is a bit hacky solution, yet its simplicity prompted me to post it. Load package and make up a data set:

Needs["ErrorBarPlots`"]
data = Sort@RandomReal[1, {10, 2}]; error = RandomReal[0.2, 10];

errorplot = ErrorListPlot[Partition[Riffle[data, ErrorBar /@ error], 2], 
            Joined -> True, PlotRange -> All, Frame -> True, Axes -> False]

enter image description here

IMPORTANT: nothing goes below x-axis - not the data, not the error bars. Otherwise your log-scale will break - you cannot take log of negative numbers.

Now lets take a look at the "guts" of the produced graphics:

errorplot // InputForm

enter image description here

Line graphics primitive (sometimes with Offset) applied to sets of points given by coordinates like {x, y}. You just need to replace all these pairs by {x, Log@y}. Careful with Offset - its 1st argument needs to be left a lone. Luckily for us it has an integer 0 so it is easy to avoid applying a pattern that distinguishes it from real numbers we need to deal with.

So here is your one-liner solution:

lerrorplot = errorplot /. {x_Real, y_Real} -> {x, Log@y}

enter image description here

Notice undesirable non-standard ticks on vertical axes (corresponding to log values). To check that it is indeed correct - compare versus ListLogPlot:

check = ListLogPlot[data, Joined -> True, Frame -> True, 
Axes -> False, PlotStyle -> {Thickness[.03], Orange, Opacity[.3]}];
Show[check, lerrorplot, PlotRange -> All]

enter image description here

A perfect match. Notice the ticks on vertical axes now are in traditional log-scale type (corresponding to original un-scaled data). Of course, your error bars got log-scaled too. Warning: be careful with these ReplaceAll type of solutions - you may be up to a surprise to what exactly is getting replaced. So always analyse your code to avoid unpleasant urprises.

+1, for a straightforward solution. Looking at the code for ErrorListPlot, it uses ReplaceAll to effect its changes. Although it is a little more thorough and discriminating in it's approach. — rcollyer, Apr 04 '12 at 13:31
Nice answer. BTW I liked the ripped-out look of your InputForm picture; Mathematica? It's ideal for pictures that have to convey the message "There's more of this, but that's not important". — Sjoerd C. de Vries, Apr 04 '12 at 13:40
@SjoerdC.deVries I use the software is called Snagit. It'd be cool to implement it in Mathematica. — Vitaliy Kaurov, Apr 04 '12 at 16:30
Thanks very much, I ended up using the ErrorBarLogPlot package linked by @Markus Roellig since in the end I need a log-log plot. I tried lerrorplot = errorplot /. {x_Real, y_Real} -> {Log@x, Log@y} but I just got a green box. — s0rce, Apr 04 '12 at 19:25

score 20 · Accepted Answer · edited Apr 04 '12 at 19:28

20

I always use the package ErrorBarLogPlots. From the website:

ErrorBarLogPlots.m is a package which adds log-scale plotting functions similar to the standard ErrorListPlot provided in Mathematica 6. The added functions are ErrorListLogPlot, ErrorListLogLinearPlot, and ErrorListLogLogPlot."

edited Apr 04 '12 at 19:28

rm -rf

88,781
21
293
472

answered Apr 04 '12 at 07:22

Markus Roellig

7,703
2
29
53

Strange...Once I write: Needs["ErrorBarLogPlots.m´"], I get the following error: Needs::cxt: Invalid context specified at position 1 in Needs[ErrorBarLogPlots.m.b4]. A context must consist of valid symbol names separated by and ending with `. >> ... Am I doing something wrong? – Lady InRed Nov 30 '12 at 13:35
@AnastasiiaAnishchenko Just write Needs["ErrorBarLogPlots`"]. – Markus Roellig Nov 30 '12 at 17:58
this doesn't work either...does one have to install anything in addition? I get this message: Needs::nocont: Context ErrorBarLogPlots` was not created when Needs was evaluated. >> – Lady InRed Dec 03 '12 at 14:21
@AnastasiiaAnishchenko Hmm, I don't get this error. Have you installed the package? Here is the link . Download the zip file and install it, then retry the Needs command. – Markus Roellig Dec 04 '12 at 09:40
1

This solution may no longer work correctly in version 8 and above, as suggested in this question – Jens Aug 16 '13 at 17:36
This runs in 11.3.0.0. It is in my "init.m" file and one of the first packages i install on a new machine. Added this because the link to "this question" gave me a 404. – xsk8rat Aug 14 '18 at 01:19

drgrujic · Answer 4 · 2016-12-08T09:02:33.827

According to solution of Dr. Belisarius I wrote this more convenient code:

(* default options needed for error plot *)
Options[errListPlot] = {
   Filling -> {1 -> {2}},
   Joined -> {False, False, True},
   PlotStyle -> {Black, Black, Directive[Opacity[0.6], Blue]},
   FillingStyle -> Black,
   PlotMarkers -> {Graphics@Line[.04 {{-1, 0}, {1, 0}}], 
     Graphics@Line[.04 {{-1, 0}, {1, 0}}], ""}
   };
(*
plotFun - any ListPlot familly function;
data =List ( x, y, error );
opts - usual ListPlot options;
*)
errListPlot[plotFun_, data_, opts : OptionsPattern[]] := Block[{},
  plotFun[{{#[[1]], #[[2]] - #[[3]]} & /@ 
     data, {#[[1]], #[[2]] + #[[3]]} & /@ data, data[[;; , {1, 2}]]}, 
   opts, Sequence @@ Options[errListPlot]]
  ]
data = Table[{i, RandomReal[10], RandomReal[{0.1, 1}]}, {i, 1, 20}];
errListPlot[ListLogPlot, data, PlotRange -> All, Frame -> True, 
 FrameLabel -> {"x label", "y label"}, ImageSize -> 800, 
 BaseStyle -> {18, FontFamily -> "Arial"}]

First I set necessary options for the plot with Options[errListPlot]. Then the plot function is defined with option pattern. Supplied options will be given to targeted List-XXX-Plot function and applied to the graphics.

Be careful, supplied option will overwrite default options from Options[errListPlot]. This can be useful if you do it right or catastrophic.

The question requested that the y-axis be logarithmic, not the x-axis. — bbgodfrey, Jul 22 '16 at 17:06
This solution works for any combination of log, loglog, loglinear, linearlog plots. Example ListLogPlot: errListPlot[ListLogPlot, data]. — drgrujic, Jul 25 '16 at 15:23
In that case, you may wish to edit your answer to include a figure that responds directly to the question. Doing so would make your answer more useful to others. Best wishes. — bbgodfrey, Jul 25 '16 at 15:35

score 5 · Answer 5 · answered Apr 18 '19 at 02:54

5

In Mathematica 12, the ErrorBarPlots package was replaced by the built-in Around function and related methods.

Now it's possible to display errorbars on a logarithmic plot using only built-in core functions and the ListLogPlot function:

data = Sort@RandomReal[{2, 5}, {10, 2}];
error = RandomReal[0.5, 10];
toPlot = MapThread[({#1[[1]], Around[#1[[2]], #2]}) &, {data, 
    error}];
ListLogPlot[toPlot, Joined -> True, Frame -> True]

answered Apr 18 '19 at 02:54

balping

438
5
7

Unfortunately, this will always plot the absolute uncertainties. In Log-scale it is common to plot the relative error to avoid funny artifacts. ErrorBarLogPlots automatically took care of this. Does anybody found a similar functionality in V12? – Markus Roellig Apr 29 '19 at 14:56
1

@MarkusRoellig By relative uncertainty you mean ±5% for example? If so, you can use Around[x, Scaled[0.05]]. – balping Apr 30 '19 at 17:23

Plotting Error Bars on a Log Scale

5 Answers5

Without using the "ErrorBarPlots`" Package

Linked