I have a such graph
graph = Graph[{1 <-> 2, 1 <-> 6, 2 <-> 3, 2 <-> 7, 3 <-> 4, 3 <-> 17,
4 <-> 5, 4 <-> 9, 5 <-> 10, 6 <-> 7, 7 <-> 17, 7 <-> 12, 17 <-> 9,
17 <-> 13, 9 <-> 10, 9 <-> 14, 11 <-> 12, 11 <-> 16, 12 <-> 13,
12 <-> 8, 13 <-> 14, 13 <-> 18, 14 <-> 24, 14 <-> 19, 24 <-> 20,
16 <-> 8, 16 <-> 21, 8 <-> 18, 8 <-> 22, 18 <-> 19, 18 <-> 23,
19 <-> 20, 19 <-> 15, 20 <-> 25, 21 <-> 22, 21 <-> 26, 22 <-> 23,
22 <-> 27, 23 <-> 15, 23 <-> 28, 15 <-> 29, 25 <-> 30, 26 <-> 27,
27 <-> 28, 28 <-> 29, 29 <-> 30}]

I hope to make it GridEmbedding exactly,which mean all vertex in a regular rectangle shape.Of course if we use VertexCoordinates to specify every position for those vertices,but that will be little troublesome.If I specify a layout of "GridEmbedding" directly,the result always will be depressed like
{PlanarGraph[graph, GraphLayout -> "GridEmbedding"],
Graph[graph, GraphLayout -> "GridEmbedding"]}

I even think this is a bug behavior behind method "GridEmbedding".Ok,let's reluctant to sepcify the "Dimension"(Sometimes we don't know the "Dimension" when we deal with a large graph).
Graph[graph, GraphLayout -> {"GridEmbedding", "Dimension" -> {5, 6}}]

It will be more messy.Actually we'd better don't specify the dimension of the grid graph,and a layout like this is expected

Update
I'm afraid to make this qeustion too board, but I have to say the current method I have received,include myself try, will fail when we delete the 7 <-> 12 and 17 <-> 13 from graph.
graph = Graph[{1 <-> 2, 1 <-> 6, 2 <-> 3, 2 <-> 7, 3 <-> 4, 3 <-> 17,
4 <-> 5, 4 <-> 9, 5 <-> 10, 6 <-> 7, 7 <-> 17, 17 <-> 9, 9 <-> 10,
9 <-> 14, 11 <-> 12, 11 <-> 16, 12 <-> 13, 12 <-> 8, 13 <-> 14,
13 <-> 18, 14 <-> 24, 14 <-> 19, 24 <-> 20, 16 <-> 8, 16 <-> 21,
8 <-> 18, 8 <-> 22, 18 <-> 19, 18 <-> 23, 19 <-> 20, 19 <-> 15,
20 <-> 25, 21 <-> 22, 21 <-> 26, 22 <-> 23, 22 <-> 27, 23 <-> 15,
23 <-> 28, 15 <-> 29, 25 <-> 30, 26 <-> 27, 27 <-> 28, 28 <-> 29,
29 <-> 30}, VertexLabels -> "Name"]

I think the Annealing algorithm can serve here, but I don't know how to implement it.







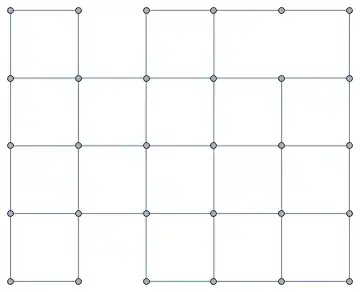

"GridEmbedding"or not?Then I can decide to add abugtag. – yode Apr 28 '17 at 07:14