How to find those missing edges in a grid graph

Question

I want to find a new method for this question.Suppose I have a such graph

graph = Graph[{1 <-> 2, 1 <-> 6, 2 <-> 3, 2 <-> 7, 3 <-> 4, 3 <-> 17, 
   4 <-> 5, 4 <-> 9, 5 <-> 10, 6 <-> 7, 7 <-> 17, 7 <-> 12, 17 <-> 9, 
   17 <-> 13, 9 <-> 10, 9 <-> 14, 11 <-> 12, 11 <-> 16, 12 <-> 13, 
   12 <-> 8, 13 <-> 14, 13 <-> 18, 14 <-> 24, 14 <-> 19, 24 <-> 20, 
   16 <-> 8, 16 <-> 21, 8 <-> 18, 8 <-> 22, 18 <-> 19, 18 <-> 23, 
   19 <-> 20, 19 <-> 15, 20 <-> 25, 21 <-> 22, 21 <-> 26, 22 <-> 23, 
   22 <-> 27, 23 <-> 15, 23 <-> 28, 15 <-> 29, 25 <-> 30, 26 <-> 27, 
   27 <-> 28, 28 <-> 29, 29 <-> 30}, VertexLabels -> "Name"]

Mathematica graphics

How to find those missing edges,such as {6<->11,10<->24,15<->25}?

Let's make this more specific. So you have a subgraph of a grid graph, where some of edges were dropped, but all of the vertices were kept? — Szabolcs, May 07 '17 at 11:50
May graph be a subset of multiple grids, or is there enough edges for uniqueness of the solution? — Coolwater, May 07 '17 at 12:38

kglr · Answer 1 · 2017-05-07T22:26:19.910

5

gg = GridGraph[{5, 6}, VertexLabels->"Name"];

isomorphisms = DeleteCases[FindGraphIsomorphism[graph, #] & /@ 
     (EdgeDelete[gg, #] & /@ 
      Subsets[EdgeList[gg], {EdgeCount[gg] - EdgeCount[graph]}]), {}];
vmap = First@MinimalBy[Join@@DeleteCases[Normal @ isomorphisms, Rule[x_, x_], 3], Length];

ed = Complement[EdgeList[gg], EdgeList[graph] /. vmap]

{6 <-> 11, 10 <-> 15, 24 <-> 25}

SetProperty[VertexReplace[EdgeDelete[gg, ed], vmap], 
 {VertexLabels -> "Name", GraphLayout -> {"GridEmbedding", "Dimension" -> {5, 6}}}]

Mathematica graphics

edited May 07 '17 at 22:26

answered May 07 '17 at 21:54

kglr

394,356
18
477
896

Just one question,I dont' know that dimension {5, 6} in some larger graph by a glance. – yode May 08 '17 at 17:23

score 2 · Answer 2 · answered May 07 '17 at 14:29

The graph is a subgraph of same dimension grid graph. The basic idea is to find the corresponding grid graph's edges which are not in the subgraph's edge list.

If it's necessary, please refer to How to make a graph be a grid layout exactly?

In:

xss = {1 <-> 2, 1 <-> 6, 2 <-> 3, 2 <-> 7, 3 <-> 4, 3 <-> 17, 4 <-> 5,
    4 <-> 9, 5 <-> 10, 6 <-> 7, 7 <-> 17, 7 <-> 12, 17 <-> 9, 
   17 <-> 13, 9 <-> 10, 9 <-> 14, 11 <-> 12, 11 <-> 16, 12 <-> 13, 
   12 <-> 8, 13 <-> 14, 13 <-> 18, 14 <-> 24, 14 <-> 19, 24 <-> 20, 
   16 <-> 8, 16 <-> 21, 8 <-> 18, 8 <-> 22, 18 <-> 19, 18 <-> 23, 
   19 <-> 20, 19 <-> 15, 20 <-> 25, 21 <-> 22, 21 <-> 26, 22 <-> 23, 
   22 <-> 27, 23 <-> 15, 23 <-> 28, 15 <-> 29, 25 <-> 30, 26 <-> 27, 
   27 <-> 28, 28 <-> 29, 29 <-> 30};
graph = Graph[xss, VertexLabels -> "Name"]

(*thanks for yode's code to get the dimension*)

spiralGraph = Graph[xss, GraphLayout -> "DiscreteSpiralEmbedding"];
dimension = 
  Length@*Union /@ Transpose[GraphEmbedding[spiralGraph]] // Reverse;

rules = xss // Map[First] // DeleteDuplicates // {#, Sort[#]} & // 
  MapThread[Rule, #] & (*Vertex\[Rule]Index Rules*)

List @@@ (xss /. rules) // UndirectedEdge @@@ # & // 
 Graph[#, VertexLabels -> "Name"] &

(*Transformed subgraph*)
sg = 
 List @@@ (xss /. rules) // UndirectedEdge @@@ # & // 
  Graph[#, VertexLabels -> "Name"] &
(*Grid Graph*)
gg = GridGraph[dimension, VertexLabels -> Reverse@rules]

{gg, sg} // Map[EdgeList] // Sequence @@ # & // Complement // 
 Map[# /. rules &]

Out:

Thanks very much. I just always fail to understand your xss // Map[First] // DeleteDuplicates // {#, Sort[#]} &..though I have to say this is very usefull method. — yode, May 09 '17 at 13:20

Szabolcs · Accepted Answer · 2017-05-08T16:15:32.730

If only edges are missing, you can first generate a list of candidate grid graphs with the same number of nodes as in graph, then see which one contains graph as a subgraph. IGraph/M has subgraph finding functionality.

It could be derived from any of these grids, as they all have the same number of nodes:

candidateGrids =
 With[{vc = VertexCount[graph]},
  GridGraph[{#, vc/#}] & /@ Select[Divisors[vc], # <= Sqrt[vc] &]
 ]

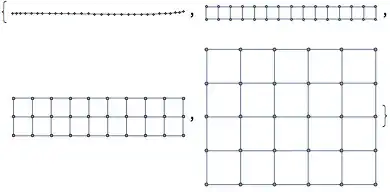
Mathematica graphics

Select the first one of these which contains graph as a subgraph:

<< IGraphM`
completeGrid = SelectFirst[candidateGrids, IGSubisomorphicQ[graph, #] &]

We can find one mapping between the vertices of graph and completeGrid using IGVF2GetSubisomorphism:

mapping = First@IGVF2GetSubisomorphism[graph, completeGrid]
(* <|1 -> 1, 2 -> 2, 6 -> 6, 3 -> 3, 7 -> 7, 4 -> 4, 17 -> 8, 
 5 -> 5, 9 -> 9, 10 -> 10, 12 -> 12, 13 -> 13, 14 -> 14, 11 -> 11, 
 16 -> 16, 8 -> 17, 18 -> 18, 24 -> 15, 19 -> 19, 20 -> 20, 21 -> 21, 
 22 -> 22, 23 -> 23, 15 -> 24, 25 -> 25, 26 -> 26, 27 -> 27, 28 -> 28,
  29 -> 29, 30 -> 30|> *)

Then you can retrieve whatever you like: vertex coordinates, missing edges, etc.

coords = PropertyValue[{completeGrid, #}, VertexCoordinates] & /@ 
  Lookup[mapping, VertexList[graph]]

SetProperty[
 graph,
 VertexCoordinates -> Thread[VertexList[graph] -> coords]
]

Mathematica graphics

Or missing edges:

reverseMapping = Reverse /@ Normal[mapping];

missing =
 Block[{UndirectedEdge},
  SetAttributes[UndirectedEdge, Orderless];
  Complement[
   EdgeList[completeGrid] /. reverseMapping,
   EdgeList[graph]
   ]
  ]
(* {6 <-> 11, 10 <-> 24, 15 <-> 25} *)

(The Orderless attribute is temporarily set on UndirectedEdge to make sure that a <-> b is considered the same as b <-> a.)

HighlightGraph[
 VertexReplace[completeGrid, reverseMapping],
 missing,
 GraphHighlightStyle -> "Dashed",
 Options[completeGrid, GraphLayout]
 ]

Mathematica graphics

This will, of course, be quite slow due to the difficulty of finding subgraphs. It will only work well for small grids like the one in your example.

To get all possible mappings instead of just one, use IGVF2FindSubisomorphisms. There will always be at least 4 possible mapping due to the symmetries of grid graphs.

How to find those missing edges in a grid graph

3 Answers3

Linked