24

This not-well-documented option of Compile has been used quite a bit in this site, and based on these examples, I used to think "InlineExternalDefinitions" -> True only works for

  1. Compilable numbers
  2. Compilable pure functions
  3. Compiled functions

until the day I was astonished by George Varnavides: “Symmetry in Chaos” (128 characters). In this example, a non-numeric Symbol is inlined! The relevant part can be boiled down to the following example:

a = #;
cf = Compile[{c}, Nest[a &, c, 10],
  CompilationOptions -> {"InlineExternalDefinitions" -> True}];

<<"CompiledFunctionTools`"
CompilePrint@cf

So my question is,

  1. Is this example just a special case, or it represents a family of expressions that can be inlined by "InlineExternalDefinitions" -> True?

  2. Is there other type(s) of inlineable expressions? Has anyone already summarized it?

P.S. George's code piece is quite tricky, if you have trouble in understanding it, consider posting a new question like "why does George's code work?".

xzczd
  • 65,995
  • 9
  • 163
  • 468
  • From my experience what are usually inlined are other compiled functions. Their code is copied into the main function everytime they are called by the main function. – faysou Jun 05 '17 at 07:37
  • @faysou Yeah as mentioned in the question that's one type of inlineable expressions I was aware of. What I'm interested is, 1. Are there more? 2. Is there a simple rule for judging whether a expression can be inlined or not? – xzczd Jun 05 '17 at 08:51
  • 1
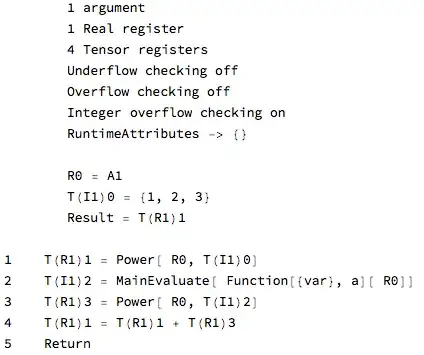
    "InlineExternalDefinitions" -> True is very similar to using With. For example f1 = Sin[x^2]; cf1 = Compile[ {{x}}, f1, CompilationOptions -> {"InlineExternalDefinitions" -> True}]; CompilePrint[ cf1] (a case not covered by your list) is like using With[{f2 = Sin[x^2]}, cf2 = Compile[ {{x}}, f2, CompilationOptions -> {"InlineExternalDefinitions" -> False}]; CompilePrint[ cf2] ]. There might be special cases (recursion?) were this analogy fails. – Karsten7 Jun 05 '17 at 11:42
  • 1
    @Karsten7. 1. The first example you gave is surprising! (BTW, though not related to the topic, another surprising thing is, With[{mid = Sin[x^2]}, Compile[{x}(*notice the seemingly trivial modification here*), mid]] // CompilePrint isn't compiled. ) 2. I think "InlineExternalDefinitions"->True isn't that similar to Evaluate or HoldAll, because e.g. f1 = Sin[x^2]; cf = Compile[{{x, _Real, 1}}, First[f1], CompilationOptions -> {"InlineExternalDefinitions" -> True}]; CompilePrint[cf] can't be implemented with these technique. – xzczd Jun 05 '17 at 12:11
  • @Karsten7. Just noticed halirutan has told me this before but I forgot about it, Oh…: http://chat.stackexchange.com/transcript/message/35824353#35824353 – xzczd Jun 05 '17 at 12:17
  • 2
    Btw, the behavior of "InlineExternalDefinitions" -> True even changed between v9 and v10. – Karsten7 Jun 05 '17 at 12:59
  • @Karsten7. I think you can summarize your comments to an answer, it does (at least partly) answer my question. – xzczd Jun 11 '17 at 05:25

2 Answers2

6

In general, investigating this features is mostly trial and error, because Compile is a pure kernel function that resists inspection by PrintDefinitions or Trace. Therefore, the only reliable source of information are the one example from the documentation and trying things out. What follows is list of rules extended from my comments.

What can be inlined by "InlineExternalDefinitions" -> True?

In principle, basic own values (see OwnValues) created using Set can potentially be inlined by "InlineExternalDefinitions" -> True.

ext1 = 1;
ext2 = Pi;
ext3 = #;
ext4 = Sin[x];
ext5 = Compile[{x}, Cos[x]];
ext6 = #^2 &;

cf = Compile[{{x, _Real, 0}},
  ext1*ext2 + Nest[ext3 &, x, 10] + ext6[ext4*ext5[x]]
  , CompilationOptions -> {"InlineExternalDefinitions" -> True}
  ]

Needs["CompiledFunctionTools`"];
CompilePrint@cf

Also the DownValues of indexed objects (the DownValues with a single match) can become inlined.

extDV1[1] := 1;
extDV2[1] = 1;
extDV3[y] = x;

cf2 = Compile[{{x, _Real, 0}}, extDV1[1] + extDV2[1] + extDV3[y], 
  CompilationOptions -> {"InlineExternalDefinitions" -> True}]
CompilePrint@cf2

What can't be inlined by "InlineExternalDefinitions" -> True?

Everything else, especially OwnValues created by SetDelayed and DownValues that rely on pattern matching, can't be inlined by "InlineExternalDefinitions" -> True.

ext7 := 1;
cf3 = Compile[{{x, _Real, 0}},
  ext7*x
  , CompilationOptions -> {"InlineExternalDefinitions" -> True}
  ]

CompilePrint@cf3


ext8[x_] := x;
cf4 = Compile[{{x, _Real, 0}},
  ext8[x]
  , CompilationOptions -> {"InlineExternalDefinitions" -> True}
  ]

CompilePrint@cf4

What will be inlined?

Which DownValues will be inlined by "InlineExternalDefinitions" -> True is decided by the algorithm of Compile and is therefore hard to predict. It has even changed between version 9 and 10.

Wolfram Technical Support: "According to the developers, nPara is not inlined because Mathematica is making the conservative assumption that nPara might change in the future."

How to force inlining?

Karsten7
  • 27,448
  • 5
  • 73
  • 134
  • I donated a small introduction and as you have already commented on the issue, I really appreciate that you stepped up and wrote an answer. +1 – halirutan Jun 12 '17 at 15:03
  • @halirutan Thank you, I appreciate it. I was hoping someone would provide a more profound answer. My comments mainly expressed my own confusion and were intended to add some more aspects to the question. – Karsten7 Jun 12 '17 at 15:21
  • I'll add some more content to the last two sections later. – Karsten7 Jun 12 '17 at 15:21
  • Here comes a strange (and buggy?) exception of SetDelayed…: https://mathematica.stackexchange.com/q/158186/1871 – xzczd Oct 19 '17 at 14:32
1

Here is another contribution to the deciphering of "InlineExternalDefinitions"->True through trial and error. It may inline the first instance of a symbol but fail to do so for the second, as in the following example:

ClearAll[a, cf];
a = Range[3];
cf = Compile[{{var, _Real}},
   var^a + var^a,
   {{a, _Integer, 1}},
   CompilationTarget -> "C", 
   CompilationOptions -> {"InlineExternalDefinitions" -> True}];
CompilePrint@cf

enter image description here

a clearly was inlined into T(I1)0, and used in line 1 of the printout, but was then obtained by a call to MainEvaluate to be used in the second term.

xzczd
  • 65,995
  • 9
  • 163
  • 468
FalafelPita
  • 845
  • 5
  • 16