7

I have constructed a BSplineFunction through a set of random points:

p = Table[{20 Cos[2 π t], 20 Sin[2 π t]} + RandomReal[{-15, 15}, 2],
          {t, 0, 0.9, 0.1}]
f = BSplineFunction[p, SplineClosed -> True];

{{15.7336, -3.557}, {11.1177, -2.53343}, {15.4259, 19.1467}, {6.60292, 10.5131},
 {-28.5053, 10.9099}, {-22.7909, -1.35239}, {-3.22756, -13.0483},
 {-17.1309, -32.426}, {6.23965, -7.05847}, {25.0532, -25.0634}}

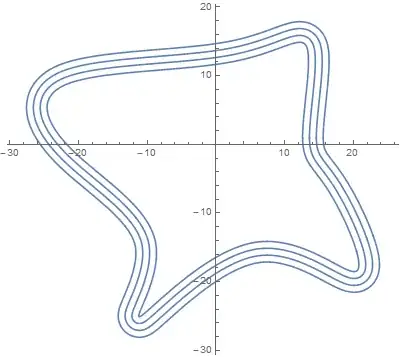
I then drew the spline and 3 curves parallel to it:

Show[ParametricPlot[Table[f[x] + {{0, 1}, {-1, 0}}.Normalize[f'[x]] * i,
                          {i, 0, 3}], {x, 0, 1}]]

spline and parallels

I next wanted to find the length of these curves, but the following command can only find the length of the spline, not the adjacent curves. It gives an error for the other curves.

Table[NIntegrate[Norm[D[f[x] + {{0, 1}, {-1, 0}}.Normalize[f'[x]]*i, x]],
                 {x, 0, 1}], {i, 0, 3}]

{148.521,(*Unevaluated Expression*),
 (*Unevaluated Expression*),(*Unevaluated Expression*)}

Attempting to solve my problem, I found that my difficulty seems to be in getting Mathematica to calculate the derivative first before substituting in values during the integration step. E.g. this does not evaluate to a value:

D[f[x] + {{0, 1}, {-1, 0}}.Normalize[f'[x]], x] /. x -> 0.5
{23.4356 - 4.78553 Norm'[{28.2999, -155.368}],
 -134.177 - 3.79751 Norm'[{28.2999, -155.368}]}

If my function was explicit, I know how to fix this, but given that my function isn't explicitly defined, I find my knowledge of Mathematica is lacking to fix this.

For reference if required, I am using version 10.2.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Ian Miller
  • 393
  • 1
  • 11

1 Answers1

6

Combining the results from this answer and this answer, here is how to get the lengths of your parallel curves:

p = {{15.7336, -3.557}, {11.1177, -2.53343}, {15.4259, 19.1467}, {6.60292, 10.5131},
     {-28.5053, 10.9099}, {-22.7909, -1.35239}, {-3.22756, -13.0483}, {-17.1309, -32.426},
     {6.23965, -7.05847}, {25.0532, -25.0634}};
m = 3; (* degree *) n = Length[p];
fn[t_] = Table[BSplineBasis[{m, ArrayPad[Subdivide[n], m, "Extrapolated"]}, j - 1, t],
               {j, n + m}].ArrayPad[p, {{0, m}, {0, 0}}, "Periodic"];

Table[NIntegrate[Sqrt[#.#] &[D[fn[t] - i #/Sqrt[#.#] &[Cross[fn'[t]]], t]], {t, 0, 1}],
      {i, 0, 3}]
   {148.52091182623133, 154.80408759110168, 161.08726314974254, 167.37043875503448}
J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
  • Thanks. I'm new to working with Splines so I'll have to read up on the difference between how you've used BSplineBasis and BSplineFunction. I like your use of Sqrt[#.#]& to replace Norm as that had been part of the problem. And Cross looks neater for doing rotations, I'll have to make use of that one in the future. – Ian Miller May 20 '17 at 09:19
  • One thing I've noticed with the change from BSplineFunction to using BSpineBasis is a significant slow down in speed. The parametric plot using my f function takes my computer around 0.25 seconds while using your fn functions takes about 15 seconds. I guess I can use both depending on the situation. – Ian Miller May 20 '17 at 09:49
  • Yes, expanding to the basis functions is a fair bit slower, but has the advantage of being more easily manipulated symbolically. So: use BSplineFunction[] for pure numerical evaluations, and the BSplineBasis[] expansion otherwise. – J. M.'s missing motivation May 20 '17 at 10:35
  • 1
    Playing with this a bit more I've found that the {0,0} inner term in ArrayPad isn't needed. – Ian Miller May 21 '17 at 05:01