11

I have a closed curve. I am trying to enclose this closed curve with another closed curve, which looks identical in the shape of the first closed curve, but slightly bigger. How to do this?

pts = {{-1, 0}, {-1, 1}, {0, 0}, {1, 1}, {1, 0}};
Graphics[{Thick, BSplineCurve[pts, SplineClosed -> True]}]
Peter Mortensen
  • 759
  • 4
  • 7
acoustics
  • 1,709
  • 9
  • 20
  • 1
    Your question is unclearly formulated: what do do you mean by 'bigger"? how about pts = {{-1, 0}, {-1, 1}, {0, 0}, {1, 1}, {1, 0}}; Graphics[{Thick, BSplineCurve[pts, SplineClosed -> True], BSplineCurve[1.1*pts, SplineClosed -> True]}]? – user64494 Aug 14 '20 at 15:34
  • Similar to the situation of this, enclosing a small rectangle by a bigger rectangle, all the side of the smaller rectangle is equal distance from the bigger rectangle – acoustics Aug 14 '20 at 15:37
  • 3
    So in short, you wanted a parallel curve / offset curve of your original curve. – J. M.'s missing motivation Aug 14 '20 at 23:15

1 Answers1

20

1. You can use BSplineFunction as follows:

pts = {{-1, 0}, {-1, 1}, {0, 0}, {1, 1}, {1, 0}};

ClearAll[explode, bsf]
explode[f_] := f[#] + #2 Cross @ Normalize[f'[#]] &;


bsf = BSplineFunction[pts, SplineClosed -> True];


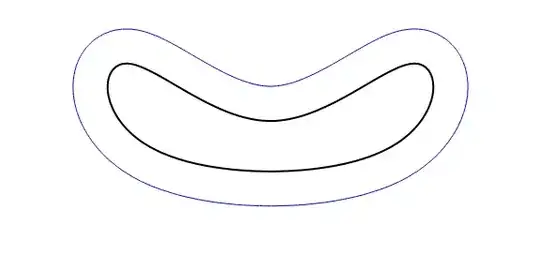
Graphics[{Thick, BSplineCurve[pts, SplineClosed -> True], Blue, 
   Line[explode[bsf][#, .2] & /@ Subdivide[100]]}] // Framed

enter image description here

Graphics[{Thick, Line[bsf /@ Subdivide[100]], Blue, 
   Line[explode[bsf][#, .2] & /@ Subdivide[100]]}] // Framed

enter image description here

2. You can also use bsf and explode with ParametricPlot:

ParametricPlot[{bsf@t, explode[bsf][t, .2], explode[bsf][t, -.1]}, {t, 0, 1}, 
 PlotStyle -> {Black, Blue, Green}, BaseStyle -> Thick, Axes -> False, 
 ImageSize -> Large]

enter image description here

3. Alternatively, you can use SignedRegionDistance + ContourPlot:

srd = Quiet @ SignedRegionDistance[Polygon[bsf /@ Subdivide[100]]];

ContourPlot[srd[{x, y}], {x, -3/2, 3/2}, {y, -.5, 1}, 
 ContourShading -> None, 
 Contours -> {{.2, Blue}, {0., {Thick, Black}}}, 
 Frame -> False, ImageSize -> Large, AspectRatio -> Automatic]

enter image description here

Use the options

ContourShading -> {PatternFilling["Grid", ImageScaled[1/10], 
  ImageScaled[{0, .35}]], None, None}

and

Epilog -> {Red, Disk[{0., .75}, .25], Black, Disk[{-.5, .8}, .1], Disk[{.5, .8}, .1]}

to get

enter image description here

Related Q/As:

kglr
  • 394,356
  • 18
  • 477
  • 896
  • It is exactly what I am looking for. Could you please explain to me how you did this? – acoustics Aug 14 '20 at 16:03
  • 1
    @acoustics, if we have a function that describes the curve (luckily we have BSplineFunction), we can use its normalized gradient to get the directions at each point on the curve (that's the Normalize @ f'[t] piece) and move each point in that direction by the desired distance. – kglr Aug 14 '20 at 16:15
  • I tried by extracting the surface normal vector at each point, then I tried scaling the points in that direction. But my results were wrong, the lines were intersecting. Anyways thanks. – acoustics Aug 14 '20 at 16:18
  • 1
    @acoustics, in general parallel curves can be self-intersecting. There is a limited range of offsets where the resulting curves do not have that property. – J. M.'s missing motivation Aug 16 '20 at 03:51