I am not sure which level cure it will be, what I have is domain and range for it which are as follows.
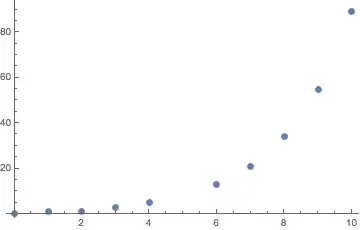
f(0) = 0
f(1) = 1
f(2) = 1
f(3) = 3
f(4) = 5
f(5) = 8
f(6) = 13
f(7) = 21
f(8) = 34
f(9) = 55
f(10) = 89
It's programmaticly tough to find out the values beyond f(10) hence is there any way i can figure it out mathematically.
As a wild guess I think is will repeat after some interval so must be a curve but any lead is appreciated !
f(8)? – Marius Ladegård Meyer Jun 02 '17 at 09:12