Evaluating what the OP tried with free-form input (shortcut =) yields a suggestion cell with this input : Expand[ InterpolatingPolynomial[{286, 771}, x]], similarly a Wolfram|Alpha query yields input interpretation interpolating polynomial, so it is not especially difficult to surmise that the desired function is InterpolatingPolynomial. Defining the list l :
l = {{1, 33}, {2, 80}, {5, 286}, {10, 771}, {15, 1382}, {20, 2087}, {25, 2867}, {30, 3707},
{40, 5526}, {50, 7470}, {60, 9482}, {70, 11507}, {80, 13495}, {90, 15391}, {100, 17313},
{110, 18631}, {120, 19752}, {125, 20064}};
the resulting polynomial (written in a standard expanded form ) is :
p[x_] := Expand @ InterpolatingPolynomial[ l, x]
How could we define an interpolating polynomial having no InterpolatingPolynomial built-in function ?
A natural way is to define recursively a family of polynomials. In order to make it possibly fast we can take advantage of memoization techiques (see e.g. answers to What is “x := x =” trickery? or Why does Expand not work within a function? )
poly[x_, 0] := l[[1, 2]]
poly[x_, k_] := poly[ x, k] = poly[ x, k-1] +
(l[[k, 2]] - poly[l[[k, 1]], k-1]) Product[(x-l[[j, 1]])/(l[[k, 1]]-l[[j, 1]]),
{j, k - 1}]
let's check if it works properly :
Expand @ poly[ x, Length @ l] === p[x]
True
Well indeed, now we can imagine what is behind InterpolatingPolynomial so let's restrict to p[x] being a seventeenth order polynomial with rational coefficients (in general when the list is of length n then the polynomial will be of order n-1, and if l is a list of rational pairs, p will be a polynomial with rational coefficients). One can reproduce the list l with p[x] :
p[#] & /@ l[[All, 1]] == l[[All, 2]]
True
Since its coefficients are a bit involved we prefer to write them this way :
p[x] // TraditionalForm // N
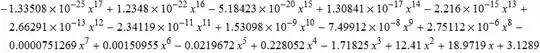
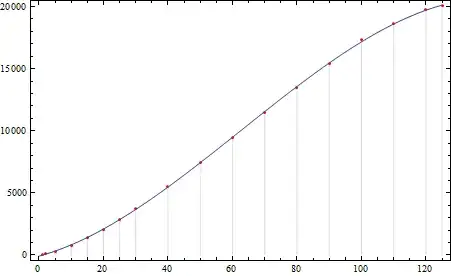
Plot[ p[x], {x, -12, 128}, PlotStyle -> Thick, Epilog -> {Red, PointSize[0.01], Point[l]}]



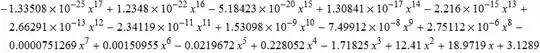

http://reference.wolfram.com/mathematica/ref/LinearSolve.html?q=LinearSolve&lang=en Or you can use the documentation center and search for Interpolation.
– Searke Oct 09 '12 at 19:11InterpolationFunctionand seeing the related functions. – rcollyer Oct 10 '12 at 12:48Interpolation[]function. – J. M.'s missing motivation Oct 10 '12 at 12:56