Why Can't Mathematica Integrate this?

Question

I have the following problem from a textbook I am trying to integrate:

So, following the directions in text, I am required to integrate each function. However, I cannot get Mathematica to integrate the first function. Here is my code:

Z1 := E^-x^2*Cos[x^2 + y^2]
Z2 := 2 - x^2 - y^2
Plot3D[{Z1, Z2}, {x, -1, 1}, {y, -1, 1}, AspectRatio -> 1, ViewPoint -> {4, 1, 1}]
Integrate[Z2, {y, -1, 1}, {x, -1, 1}] - Integrate[Z1, {y, -1, 1}, {x, -1, 1}]

They plot OK:

but give me really strange output:

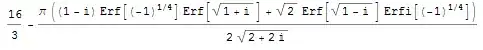
Could someone please explain how I can overcome this? Wolfram|Alpha can evaluate it without (much) trouble.

Thank you for your time.

Answer 1

Mathematica is giving you an exact symbolic result. If want a numeric integral, you should use NIntegrate instead of Integrate, or just wrap your result in N. If you want, say, 30 significant digits,

N[Integrate[Z2, {y, -1, 1}, {x, -1, 1}] - 
  Integrate[Z1, {y, -1, 1}, {x, -1, 1}], 30]

3.02706907398351331410210839012 + 0.*10^-31 I

Answer 2

You can use, in principle, Boole inside Integrate like this:

NIntegrate[
 Boole[E^-x^2 Cos[x^2 + y^2] < z < 2 - x^2 - y^2], {x, -1, 1}, {y, -1,
   1}, {z, -1, 3}]

the result is given as 3.0138472, despite warnings NIntegrate::slwcon: and NIntegrate::eincr:

I'm not able to figure out what actually happens at present, but I'm sure this way of using Boole will helps, especially for the integration of irregular regions or volumes.