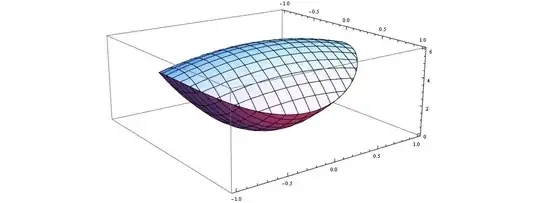
How to plot and find the volume of a solid?

Question

How to plot and find the volume of the solid enclosed between the paraboloid z=5(x^2+y^2) and z=6-7x^2-y^2

And the answer of the volume is 3Pi/(2)^1/2

Answer 1

RegionPlot3D[ 5 (x^2 + y^2) < z < 6 - 7 x^2 - y^2, {x, -1, 1}, {y, -1, 1}, {z, -0, 6}, 
             PlotStyle -> Orange, Mesh -> None, PlotPoints -> 50]

Integrate[ Boole[5 (x^2 + y^2) < z < 6 - 7 x^2 - y^2], {x, -1, 1}, {y, -1, 1}, {z, 0, 6}]
(*
 (3 π)/Sqrt[2]
*)

Answer 2

Plot3D[{5 (x^2 + y^2), 6 - 7 x^2 - y^2}, {x, -1, 1}, {y, -1, 1}, 
        RegionFunction -> Function[{x, y}, 5 (x^2 + y^2) < 6 - 7 x^2 - y^2]]

Integrate[(6 - 7 x^2 - y^2 - 5 (x^2 + y^2)) UnitStep[(6 - 7 x^2 - y^2 - 5 (x^2 + y^2))],
          {x, -10, 10}, {y, -10, 10}]

(3 π)/Sqrt[2]

Edit

Since working with the UnitStep function (rather unexpectedly) doesn't appear the most efficient approach we provide here a bit different but more obvious way exploiting HeavisideTheta.

Defer @ 
Integrate[(6 - 7 x^2 - y^2 - 5 (x^2 + y^2)) HeavisideTheta[(6 - 7 x^2 - y^2 - 5 (x^2 + y^2))],
          {x, -∞, ∞}, {y, -∞, ∞}] == 
Integrate[# HeavisideTheta[#] &[(6 - 7 x^2 - y^2 - 5 (x^2 + y^2))],
          {x, -∞, ∞}, {y, -∞, ∞}] // TraditionalForm

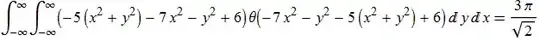
This is a faster and more elegant way than belisarius' approach in Mathematica 8 and 9

Integrate[ Boole[5 (x^2 + y^2) < z < 6 - 7 x^2 - y^2], {x, -1, 1}, {y, -1, 1}, {z, 0, 6}]//
AbsoluteTiming // First

2.228000

Integrate[ # HeavisideTheta[#] &[(6 - 7 x^2 - y^2 - 5 (x^2 + y^2))], 
          {x, -∞, ∞}, {y, -∞, ∞}] // AbsoluteTiming // First

0.245000

Warning: In Mathematica 7 there was a bug and the HeavisideTheta approach yielded an incorrect result, therefore we had to deal with UnitStep or Boole approaches.

Answer 3

The projection of your solid down to the $xy$-plane is described by $$5(x^2+y^2) \leq 6-7x^2-y^2,$$ which simplifies to $$12x^2+6y^2 \leq 6.$$ This is an equation of a solid ellipse $E$ compressed by the factor $\sqrt{2}$ in the $x$-direction. The volume can be expressed as $$\iint\limits_E (6-(12x^2+6y^2)) \, dA.$$

A truly efficient way to evaluate this integral is to work in an elliptic coordinate system: $$x=r\cos(t)/\sqrt{2}, \; y=r\sin(t).$$ In this coordinate system, the function simplifies to $6-6r^2$ and the area element is $dA=(r/\sqrt{2})\, dr \, dt$. The area element is similar to the familiar $dA = r\,dr\,d\theta$ in polar coordinates, but accounts for the extra compression in the $x$-direction. The formula can also be derived using the Jacobian.

Using this coordinate system, the integral can now be expressed as $$\int_0^{2\pi} \int_0^1 (6-6r^2)r/\sqrt{2} \, dr\, dt = 3\pi/\sqrt{2},$$ which is quite easy to do by hand.

We can also use this point of view to make a nice image:

With[{x = r*Cos[t]/Sqrt[2], y = r*Sin[t]},
  solid = ParametricPlot3D[{
     {x, y, 5 (x^2 + y^2)},
     {x, y, (6 - 7 x^2 - y^2)}
     }, {r, 0, 1}, {t, 0, 2 Pi},
    PlotStyle -> {Directive[Lighter[Blue]], Directive[Orange]}];
  shell = ParametricPlot3D[{
     {x, y, 5 (x^2 + y^2)},
     {x, y, (6 - 7 x^2 - y^2)}
     }, {r, 1, 2}, {t, 0, 2 Pi},
    Mesh -> None,
    PlotStyle -> Opacity[0.4]];
  border = ParametricPlot3D[
    {Cos[t]/Sqrt[2], Sin[t], 5 (Cos[t]^2/2 + Sin[t]^2)},
    {t, 0, 2 Pi}, PlotStyle -> Directive[Thick, Black]]
  ];
Show[{solid, shell, border}, 
 PlotRange -> {{-2, 2}, {-2, 2}, {-0.2, 6.2}}]

Answer 4

I guess this is too old school.

Solve[ 5 (x^2 + y^2) == 6 - 7 x^2 - y^2, x]

{{x -> -(Sqrt[1 - y^2]/Sqrt[2])}, {x -> Sqrt[1 - y^2]/Sqrt[2]}}

Integrate[(6 - 7 x^2 - y^2) - 5 (x^2 + y^2)  ,
         {y, -1, 1},
         {x, -(Sqrt[1 - y^2]/Sqrt[2]), Sqrt[1 - y^2]/Sqrt[2]}]

(3  π)/Sqrt[2]

Thsn again if you need to show your work on your calculus homework this is how you do it.