When one has the output of a function like TreeForm, for instance:
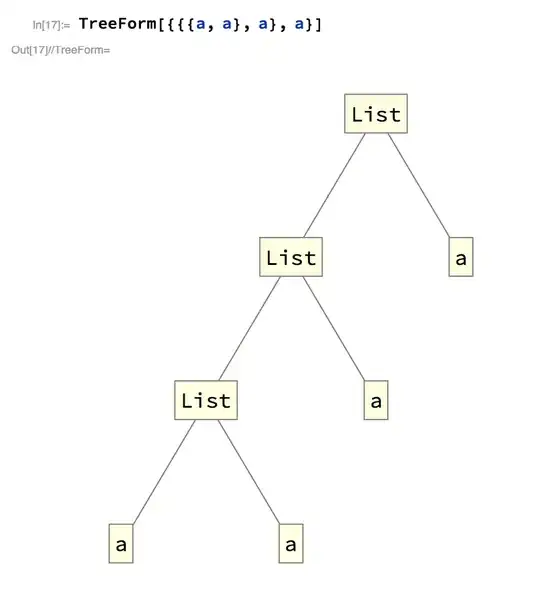
Can this be turned into a Graph object? I would like to be able to apply functions like VertexList, VertexDegree, AdjacencyList, and so on.
When one has the output of a function like TreeForm, for instance:

Can this be turned into a Graph object? I would like to be able to apply functions like VertexList, VertexDegree, AdjacencyList, and so on.
You can use halirutan's makeTree function from this answer. Your purpose is slightly different than the purpose in that question, so the function can be simplified a bit in this context:
makeTree[nodes_] := Module[{counter = 0},
traverse[h_[childs___]] := With[{id = counter},
{DirectedEdge[id, ++counter], traverse[#]} & /@ {childs}
];
traverse[_] := Sequence[];
TreeGraph[#, GraphLayout -> "LayeredDigraphEmbedding"] &@Flatten[traverse[nodes]]
]
Use it like this:
expr = TreeForm[{a, {a, {a, a, a}}}];
{expr, makeTree @@ expr}

Graph object with VertexDegree, AdjacancyList etc. I do not store the the labels (List, a), but it could be added. Other than that I don't lose any information.
– C. E.
Jul 11 '17 at 11:00
TreeFormToGraph[treeForm_] :=
Module[{tree = ToExpression@ToBoxes@treeForm, order, pos, label},
label = Cases[tree, Inset[name_, n_] :> Rule[n, Placed[name, Center]],Infinity];
{order, pos} = Catenate /@ Cases[tree,
Line[order_] | GraphicsComplex[pos_, ___] :> {order, pos}, Infinity];
Graph[UndirectedEdge @@@ order, VertexLabels -> label,
VertexCoordinates -> MapIndexed[Rule[First[#2], #] &, pos]]]
Note the result of TreeFormToGraph is Graph object.
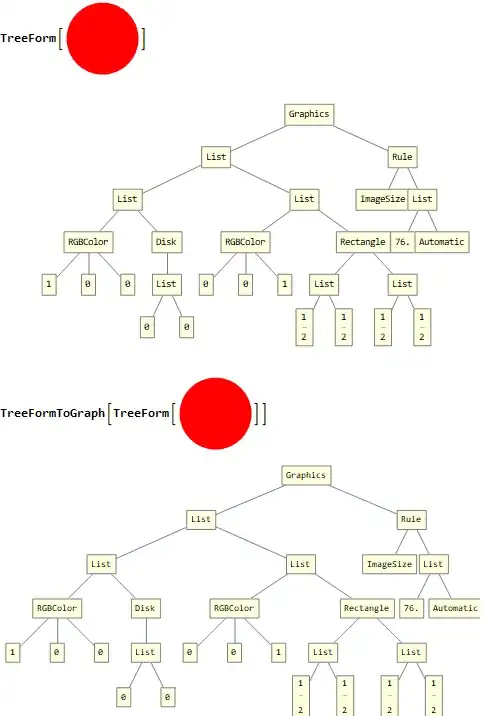

Update: We can use GraphComputation`ExpressionGraph to get a one-liner that converts a TreeForm object to a Graph object:
treeFormToGraph = Apply[GraphComputation`ExpressionGraph];
treeFormToGraph @ TreeForm[{{{a,b},c},d}]
We can add styling to get a Graph that looks like TreeForm:
ClearAll[treeFormToGraph ]
treeFormToGraph[t_TreeForm, o : OptionsPattern[]] :=
Module[{g = GraphComputation`ExpressionGraph[t[[1]], o,
VertexSize -> {"Scaled", .1}, VertexStyle -> LightYellow,
VertexShapeFunction -> "Rectangle"]},
SetProperty[g, VertexLabels -> (PropertyValue[g, VertexLabels] /.
Rule[a_, b_] :> Rule[a, Placed[b, Center]])]];
treeFormToGraph[TreeForm[{{{a,b},c},d}], VertexStyle->Pink]
Original answer:
We can use, instead of TreeForm, GraphComputation`ExpressionGraph which produces a Graph object accepting all the options of Graph.
g1 = GraphComputation`ExpressionGraph[{{{a, b}, c}, d},
VertexSize -> {"Scaled", .1}, VertexStyle -> LightYellow,
VertexShapeFunction -> "Rectangle"];
SetProperty[g1, VertexLabels -> (PropertyValue[g1, VertexLabels] /.
Rule[a_, b_] :> Rule[a, Placed[b, Center]])]
Graphics into Graph. :)
– yode
Jul 11 '17 at 20:39
TreeForm into Graph". Apply[GraphComputation`ExpressionGraph]@TreeForm[{{{a,b}, c}, d}] does it:)
– kglr
Jul 11 '17 at 21:14
This is not ideal. It requires the tree to be output. The object elements are collected and reused for a graph:
func[ex__] := (e = {}; vn = {};
TreeForm[ex,
EdgeRenderingFunction -> ({Blue, (AppendTo[e, #];
Arrow[#, .3])} &),
VertexRenderingFunction -> ((AppendTo[vn, {#1, #2}];
Text[#2, #1]) &)])
f[x_, y_] :=
Module[{el = DeleteDuplicates[UndirectedEdge @@@ x], vl, rules},
vl = VertexList[Graph[el]];
rules = MapIndexed[#1 -> #2[[1]] &, vl];
Graph[el /. rules, VertexLabels -> Rule @@@ (y /. rules)]]
An example:
func[{a, b, {c, d}, {w, r}}] (* tree must be rendered*)
graph = f[e, vn]
IGraph/M now includes a function to convert a Mathematica expression into a Graph similar to what TreeForm would display. It is faster than GraphComputation`ExpressionGraph, especially if you turn off vertex labelling.
IGExpressionTree[{{{a, a}, a}, a}]
tree = IGExpressionTree[expr = {{{a, a}, a}, a}, VertexLabels -> None,
GraphLayout -> {"LayeredEmbedding", "RootVertex" -> {}}]
The vertex names of this tree are the positions of the corresponding subexpressions. Above, the root vertex was set to {}, which is the position specification of the entire expression.
VertexList[tree]
(* {{1, 1, 1}, {1, 1, 2}, {1, 1}, {1, 2}, {1}, {2}, {}} *)
Extract[expr, VertexList[tree]]
(* {a, a, {a, a}, a, {{a, a}, a}, a, {{{a, a}, a}, a}} *)
We could also have labelled the vertices with these subexpressions:
IGExpressionTree[expr, VertexLabels -> "Subexpression",
GraphLayout -> {"LayeredEmbedding", "RootVertex" -> {}}]
Should you need the vertex names to be just integers, use IndexGraph.
ExpressionGraph and Graph solutions -- see below for the code.Half of my answer is a 2021 update to the answer provided by Szabolcs and the answer provided by kglr. It appears that the former GraphComputation`ExpressionGraph has now been migrated to vanilla ExpressionGraph (no GraphComputation` context anymore). The posted code which previously worked doesn't translate directly into the new function, but I have performed some minor tweaks to make it work in 2021.
In addition to 2021 compatibility, I have added two features. The first feature is the ability to auto-size the VertexLabels. This includes auto-sizing the frame around the text, and setting a maximum font size, after which the text auto-shrinks. The second feature is simply some syntactic sugar to wrap some code around Graph and allow arbitrary user-specified customizations. The customizations work in a manner similar to the existing VertexLabelFunction option, and custom functions have access to all the available underlying Graph data.
I have provided one version that works with GraphComputation`ExpressionGraph and another that works with vanilla Graph, which allows a plethora of customization (e.g. via the GraphLayout option). See the reference manual pages for Graph and GraphLayout for further information.
EDIT: After re-reading the original post, I converted the code to use Graph directly instead of TreePlot (whose output is a Graph object, but the original post specifically requested the use of Graph). See the edit history if you'd like a TreePlot version; it's literally three symbols of changes (TreePlot <--> Graph wherever they appear).
Now the code...
Vanilla 2021 ExpressionGraph
ExpressionGraph[
#,
VertexLabels -> Placed[Automatic, Center],
VertexLabelStyle -> Directive[FontSize -> Scaled@0.04],
VertexStyle -> LightYellow,
VertexShapeFunction -> "Rectangle",
VertexSize -> 3/4,
ImageSize -> Large
] &@Power[Plus[a, b, c], Sqrt[c/d]]
New SizedVertices function
[Compatible with both ExpressionGraph and my new ExprTreeGraph below]
SizedVertices = Function[vertexLabels,
Function[{center, vertex, size},
With[
{
SizedInset = Inset[#, center, {Center, Center}, size*2] &,
Styled = Style[#, FontSize -> 2*144*size[[2]]/4, Black] &,
YellowFrame =
Framed[#, Background -> LightYellow, Alignment -> Center] &,
ScaledPane =
Pane[#, ImageSize -> {UpTo@Full, UpTo@Full},
Alignment -> Center, ImageSizeAction -> "ShrinkToFit"] &
},
SizedInset@
Styled@YellowFrame@ScaledPane@ToString@vertexLabels[[vertex]]
]]];
Usage:
ExpressionGraph[
#,
VertexSize -> 3/4,
VertexShapeFunction ->
SizedVertices@Cases[#, _, {-1}, Heads -> True],
ImageSize -> Large
] &@Power[Plus[a, b, c], Sqrt[c/d]]
New ExprTreeGraph Function
[Based upon Graph, but with handy defaults and a new OptionsFunction]
ClearAll@ExprTreeGraph
With[{F = Function[f, Sequence[{v, e, lbl}, f] &, HoldAll]},
Options[ExprTreeGraph] = {
"VertexFunction" -> F@v,
"EdgeFunction" -> F@Thread@Rule[e, Most@v],
"OptionsFunction" -> F@Nothing,
"VertexLabelFunction" ->
F@Thread@Rule[v, Thread@Placed[lbl, Center]],
VertexShapeFunction -> "Rectangle",
VertexSize -> 3/4,
VertexStyle -> LightYellow,
VertexLabelStyle -> Directive[FontSize -> Scaled@0.04],
GraphLayout -> "LayeredDigraphEmbedding"
}];
ExprTreeGraph[expr_, o : OptionsPattern[{ExprTreeGraph, Graph}]] :=
With[{
parts = Position[expr, _, Heads -> False],
LabelParents =
Flatten@Through@Thread[FirstPosition@Drop[#, -1, -1]]@# &,
HandleAtomic = Replace[{} -> {1}],
HeadIf = Replace[part_?(Not@*AtomQ) :> Head@part]
},
With[{v = Range@Length@parts,
e = HandleAtomic@LabelParents@parts,
lbl = Extract[expr, parts, HeadIf]
},
Graph[
OptionValue["VertexFunction"][v, e, lbl],
OptionValue["EdgeFunction"][v, e, lbl],
Sequence @@ Normal@Merge[First]@(FilterRules[#, Options@Graph] &)@{
OptionValue["OptionsFunction"][v, e, lbl],
o,
VertexLabels -> OptionValue["VertexLabelFunction"][v, e, lbl],
Options@ExprTreeGraph
}
]]]
Usage:
ExprTreeGraph@Power[Plus[a, b, c], Sqrt[c/d]]
Or:
ExprTreeGraph[
Power[Plus[a, b, c], Sqrt[c/d]],
ImageSize -> Large,
VertexLabels -> None,
OptionsFunction -> ((VertexShapeFunction -> SizedVertices[#3]) &)
]
Example output of auto-sizing function: