How can I re-create the original Graph object from Graphics object into which that Graph was converted previously?

Question

We can convert a Graph into Graphics very easily like it is shown in this answer. My question is: how to convert a Graphics object into the original Graph from which it was created? Like the g1,g2 and g3 in the following:

SeedRandom[1]
g1 = Show[RandomGraph[{6, 10}]]
Head[g1]

Graphics

g2 = GraphPlot3D[{1 -> 2, 1 -> 3, 1 -> 4, 1 -> 5, 2 -> 3, 2 -> 4, 
   2 -> 5, 3 -> 4, 3 -> 5, 4 -> 5}]

g3 = GraphPlot[{1 -> 2, 2 -> 1, 3 -> 1, 3 -> 2, 4 -> 1, 4 -> 2, 
   4 -> 4}, VertexLabeling -> True, DirectedEdges -> True]

Interesting!Why I get so many close in such a valuable post? — yode, Jun 06 '16 at 12:24
Your question as given can't be answered for the obvious reasons. You should probably ask something like: "How can I re-create the original Graph object from Graphics object into which that Graph was converted previously?" It would be a well-defined question. — Alexey Popkov, Jun 06 '16 at 18:21
@AlexeyPopkov Actually I can't distinguish the difference between both.But I have changed it as what you suggest.I hope it will be more better post. :) — yode, Jun 06 '16 at 18:32
I have edited your question in order to make it simpler and more clear. — Alexey Popkov, Jun 06 '16 at 18:40
I think this question is well reasonable and I already voted do not close it and upvoted it. The ability to convert easily from one representation to another always was (and is) the most strong advantage of Mathematica. — Alexey Popkov, Jun 06 '16 at 18:57
Shall we preserve the points' location or simply preserving the graph's topological structure will be enough? — Wjx, Jun 07 '16 at 03:51

Wjx · Accepted Answer · 2016-06-07T07:33:55.713

3

WOW! I made it!

Code first~

Graphics2Graph[g_] := 
 Module[{cd = 
    If[FreeQ[g, Line], 
     DirectedEdge @@@ (Extract[g, Position[g, Arrow[___]]] /. 
        Arrow[x_, ___] :> {First@x, Last@x}), 
     UndirectedEdge @@@ Extract[g, Position[g, Line[_]]][[1, 1]]]},
  Graph[cd, 
   VertexCoordinates -> 
    Extract[Extract[g, Position[g, GraphicsComplex[___]]][[1, 1]], 
     List /@ VertexList@Graph[cd]], VertexLabels -> "Name"]]

Graphics2Graph /@ {g1, g2, g3}

Well, the method of doing this is quite simple. After analyzed several Graph's FullForm, I realized that all the Graphics created are in the form of GraphicsComplex and all the useful information are stored in the form of either a great Line or several Arrow. The storage, fortunately, are in regular forms:

(*Line Form*)
Line[{{1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}}]

(*Arrow Form*)
Arrow[{2,1}]
Arrow[{2,3,4,5,1}]
Arrow[{1,2},0.2]

Also, I found out that in one graph, only one form will be presented. So either a graph is totally presented by Line Form or totally presented by Arrow Form.

So the only thing I'll have to do is to find out all the Line Expression or Arrow Expression and properly convert them into styled forms. The code simply do this job with Position and Extract.

Seemingly this version do is wide-range supportive~ I've tried a few examples in Graph's documentation and it seems that this function works fine. Also the speed is quite high too~

edited Jun 07 '16 at 07:33

answered Jun 07 '16 at 07:20

Wjx

9,558
1
34
70

Nice job and I found InputForm[DiscretizeGraphics[g2]] will get a very simple form.But we cann't macth it by Cases – yode Jun 08 '16 at 01:33
Try my method of Position and Extract – Wjx Jun 08 '16 at 01:35
I mean to process Graphics3D – yode Jun 08 '16 at 01:36
oh, alright. :) – Wjx Jun 08 '16 at 01:36
And SeedRandom[1] g1 = Show[Graph[RandomGraph[{6, 10}], VertexLabels -> "Name"]] Graphics2Graph[g1] seem to give some unexpected result?SeedRandom[1] g1 = Show[RandomGraph[{6, 10}]] Graphics2Graph[g1] will mix the direct or undirect? :) – yode Jun 08 '16 at 01:44
It seem that in this case, the graphics is generated using not GraphicsComplex but simple Graphics instead. Maybe in this case we can still transform it into a graph using some modification but there'll be no clear statement of which point is 1 and which is 2. So personally I will consider this form of graphics cannot be transformed back to Graph form if you want to preserve the vertexes' name. Try RandomGraph[{600,1000}] and you'll see that in this situation, even using your eyes, you can not know which point is 1 and which is 2 as they all mixed together. – Wjx Jun 08 '16 at 03:07
Make it simple and clear, Using Show will compress the data into a pure Graphics form, so it will be impossible to convert it back in general. – Wjx Jun 08 '16 at 03:11
Thanks for your vivid explaination.And I'll be at your side. – yode Jun 08 '16 at 03:47

score 0 · Answer 2 · edited Jun 16 '20 at 09:23

I made it with a non-perferct solution,but actually I don't content with it.I hope to get a general methond to do this rather than customized for every Graphics.

For g1

pos = Cases[Normal[g1], _Arrow, Infinity][[All, 1]];
rule = MapIndexed[Rule[#, First[#2]] &, 
   DeleteDuplicates@Catenate[pos]];
Graph[UndirectedEdge @@@ (pos /. rule), 
 VertexCoordinates -> Reverse /@ rule, VertexLabels -> "Name"]

The ordering of the vertices seem to been refined

For g2

data = Cases[g2, _GraphicsComplex, Infinity];
Graph3D[UndirectedEdge @@@ data[[1, 2, 1, 2, 1]], 
 VertexCoordinates -> data[[1, 1]], GraphStyle -> "SmallNetwork"]

For g3

pos = Through[{First, Last}[#]] & /@ 
   Cases[Normal[g3], _Arrow, Infinity][[All, 1]];
rule = MapIndexed[Rule[#, First[#2]] &, 
   DeleteDuplicates@Catenate[pos]];
Graph[DirectedEdge @@@ pos /. rule, 
 VertexCoordinates -> Reverse /@ rule, VertexLabels -> "Name"]

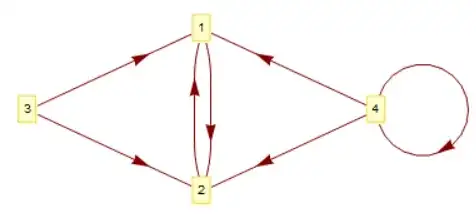
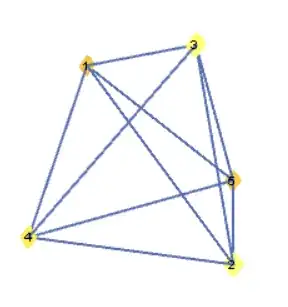
How can I re-create the original Graph object from Graphics object into which that Graph was converted previously?

2 Answers2

For g1

For g2

For g3

Linked