1

I am trying to plot this function (FvD) with respect to x. It results in an empty graph.

enter image description here

A11 = 6.8*10^-20
A22 = 5.0*10^-20
A33 = 3.7*10^-20
E0 = 8.854188
E3 = 79.99
kB = 1.38064852*10^-23
T = 298
e = 1.60217662*10^-19
z = 1
h = 6.62607004*10^-34
n00 = 6.022148086*10^24
ye1 = -35*10^-3
ye2 = -45*10^-3
A132 = (Sqrt[A11] - Sqrt[A33])*(Sqrt[A22] - Sqrt[A33])
vdW = -A132/(6*Pi*x^3)
k = 1/(Sqrt[(E0*E3*kB*T)/(2*e^2*z^2*n00)])
Y1 = (z*e*ye1)/(kB*T)
Y2 = (z*e*ye2)/(kB*T)
ElDL = n00*kB*
  T*(2*Sqrt[(1 + 0.25*(Y1 + Y2)^2*Csch[(k*x/2)]^2)] - (((Y1 - Y2)^2*
        Exp[-k*x])/(1 + 0.25*(Y1 + Y2)^2*Csch[(k*x/2)]^2)) - 2)
DisPressure = ElDL + vdW
FvD[x] = 2*Pi*(-\[Integral]DisPressure \[DifferentialD]x)
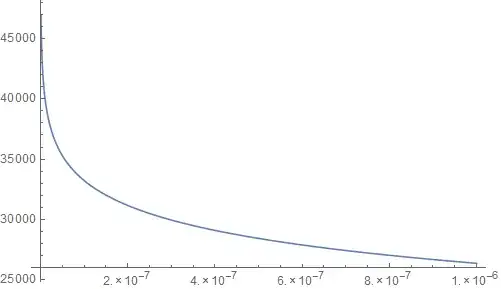
Plot[FvD[x], {x, 1*10^-9, 1000*10^-9}]

What should I do?

Askild
  • 11
  • 2
  • 3
    Post code in code blocks (use { } icon), not pictures of code. – Bob Hanlon Jul 16 '17 at 15:27
  • If I haven't made a mistake, Plot[{Re[FvD], Im[FvD]}, {x, 10^-9, 200*10^-9}] shows FvD is complex. And there is a little bit of uncertainty from the floating point constants. – Bill Jul 16 '17 at 15:35
  • Hi, I have now updated my question and the code is posted in code blocks. I am new to Mathematica and I am struggling a lot to make this plot work. – Askild Jul 17 '17 at 09:53

1 Answers1

2

  1. To define your function you need to use a Pattern in the left hand side. Reference:

  2. The output of your function is complex; see

However regarding (2) the imaginary part is nearly constant so I think you want only the real.

Apparent solution:

FvD[x_] = 2*Pi*(-∫DisPressure \[DifferentialD]x);

Plot[Re @ FvD[x], {x, 1*10^-9, 1000*10^-9}, PlotRange -> All]

enter image description here

LCarvalho
  • 9,233
  • 4
  • 40
  • 96
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • Thank you for helping me @Mr.Wizard. I have updated my code like you described above. However, now I receive this comment:

    Set::write: Tag Times in (2 \[Pi] (-(5.67161*10^-23/x^2)+49554.2 x+<<1>>/Sqrt[<<1>>]+(368.13 2.71828^(-651.462 x) <<4>> (3.85257 +Cosh[162.866 x]^2+Sinh[162.866 x]^2))/((0.412153 +1. Csch[<<1>>]^2) (-154.867 2.71828^Times[<<2>>] <<4>> Sinh[Times[<<2>>]] (-1.+Power[<<2>>]+Power[<<2>>])+<<6>>+<<20>> <<5>> (<<1>>)))))[x_] is Protected.

     – Askild Jul 17 '17 at 10:54
  • @Askild You should restart Mathematica (or at least the Kernel) before evaluating the modified code. If you still receive that error please see https://mathematica.stackexchange.com/q/11982/121 (ps: I just noticed that I uploaded a slightly different plot; I have corrected that so that it agrees with the code in my answer above.) – Mr.Wizard Jul 17 '17 at 11:22