Increasing the thickness of minimum of two curves while keeping their coloring the same

Question

Let's say I am plotting

Plot[{Sin[x], Cos[x]}, {x, 0, 2 π}, PlotStyle -> {Thickness[0.01], Thickness[0.01]}]

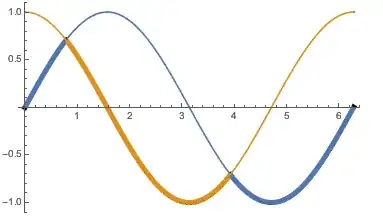
I want to keep the same colors for the two functions — $\sin(x)$ and $\cos(x)$ — but want to increase the thickness of the minimum of two functions for each value of $x$. What is the easiest way to do that?

Edit

I want to clarify what I meant. Let's say the colors of the two functions f1 and f2 are blue and red and thickness for both functions is 0.01. Now for each x, I just want to increase the thickness of the function $min(f1, f2)$ in the same plot while keeping the blue and red colors separately for f1 and f2.

Do you mean you want varying thickness along the curve, depending on which curve is on top? — Thies Heidecke, Jul 26 '17 at 12:43
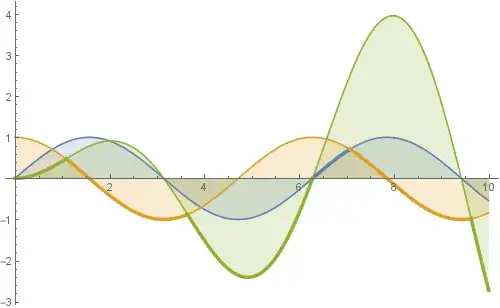
You could either achieve this by calling Plot[{Min[f1[x],f2[x]],Max[f1[x],f2[x]]}] and giving it different PlotStyles or by cutting the curves in segments where they cross and giving them individual PlotStyles. — Thies Heidecke, Jul 26 '17 at 12:51
@kglr Oh, that's another good related one, but I don't think it's a direct solution to this one? — Mr.Wizard, Jul 26 '17 at 13:56
@Mr.Wizard, this answer in the linked q/a works for this case too. — kglr, Jul 26 '17 at 14:07

yohbs · Answer 1 · 2017-07-26T13:32:35.960

Choose two colors:

{c1,c2}={ColorData[97, 1], ColorData[97, 2]}

Define a custom color function:

myColorFunction[x_] := If[Cos[x] > Sin[x], c1,c2]

Generate two plots (because you can't specify two different color functions in the same plot) and combine them:

g1 = Plot[{Sin[x], Cos[x]}, {x, 0, 2 Pi}, PlotStyle -> {c1,c2}];
g2 = Plot[Min[Sin[x], Cos[x]], {x, 0, 2 Pi}, 
   PlotStyle -> Thickness[0.015], ColorFunctionScaling -> False, 
   ColorFunction -> (myColorFunction[#1] &), Exclusions -> None];
Show[g2, g1, PlotRange -> {-1,1}]

Voilà:

m_goldberg · Accepted Answer · 2017-07-26T13:39:50.100

7

Perhaps this is what you are looking for.

minSin[x_] /; Sin[x] < Cos[x] := Sin[x]
minCos[x_] /; Sin[x] > Cos[x] := Cos[x]
maxSin[x_] /; Sin[x] > Cos[x] := Sin[x]
maxCos[x_] /; Sin[x] < Cos[x] := Cos[x]

Plot[{minSin[x], maxSin[x], minCos[x], maxCos[x]}, {x, 0, 2 π},
  PlotStyle ->
    {{Blue, Thickness[0.02]}, {Blue, Thickness[0.01]},
     {Red, Thickness[0.02]}, {Red, Thickness[0.01]}}]

edited Jul 26 '17 at 13:39

answered Jul 26 '17 at 12:39

m_goldberg

107,779
16
103
257

Thies Heidecke · Answer 3 · 2017-07-26T15:22:09.943

7

One way of doing this which works in this case would be:

Plot[Evaluate[MinMax[{#1, #2}]], {x, 0, 2 \[Pi]}, 
  PlotStyle -> {Thickness[0.01], Thickness[0.02]}, 
  ColorFunctionScaling -> False, 
  ColorFunction -> (ColorData[97][1 + Boole[Sin[#1] == #2]] &)
] &[Sin[x], Cos[x]]

edited Jul 26 '17 at 15:22

answered Jul 26 '17 at 12:59

Thies Heidecke

8,814
34
44

3

I think this doesn't answer the OP's question - the intention was to keep the colors but vary the thickness. – yohbs Jul 26 '17 at 13:31
1

Fixed my answer. – Thies Heidecke Jul 26 '17 at 15:23
1

That's very nice. – Mr.Wizard Jul 26 '17 at 15:35

kglr · Answer 4 · 2017-07-26T14:23:34.160

7

Modifying this answer slightly:

flist = {Sin[x], Cos[x]};
pieces = Table[ConditionalExpression[f, f == Min[flist]], {f, flist}];
pltstyls = Join[#, Directive[{#, Thickness[.007]}] & /@ #] &[
  ColorData[97, "ColorList"][[;; Length@flist]]];

Plot[Evaluate@Join[flist, pieces], {x, 0, 10}, PlotStyle -> pltstyls]

More generally, for arbitrary number of functions and filling:

flist = {Sin[x], Cos[x], x Sin[x]/2};
filling = Thread[Range[Length@flist] -> Axis];
pieces = Table[ConditionalExpression[f, f == Min[flist]], {f, flist}];
pltstyls = Join[#, Directive[{#, Thickness[.007]}] & /@ #] &[
  ColorData[97, "ColorList"][[;; Length@flist]]];

Plot[Evaluate@Join[flist, pieces], {x, 0, 10}, Filling -> filling, PlotStyle -> pltstyls]

edited Jul 26 '17 at 14:23

answered Jul 26 '17 at 14:16

kglr

394,356
18
477
896

I think the filling and the third line obfuscate this somewhat, but +1 nevertheless. – Mr.Wizard Jul 26 '17 at 14:17
Thank you @Mr.Wizard. – kglr Jul 26 '17 at 14:24

score 2 · Answer 5 · answered Jul 26 '17 at 14:35

Applying a modification of my own method from Plot the minimum of a list of functions, and perhaps proving kglr's assertion that this question is a duplicate:

emph[fn_][a__] := Riffle[{a}, If[# == fn[a], #] & /@ {a}]

Plot[emph[Min][Sin[x], Cos[x]], {x, 0, 2 Pi}
 , Evaluated -> True
 , PlotStyle -> Tuples[{{Blue, Red}, AbsoluteThickness /@ {2, 4}}]
]

Increasing the thickness of minimum of two curves while keeping their coloring the same

Edit

5 Answers5