Use different ColorFunction for each function plotted

Question

When plotting two curves on one plot, you can specify different colors for each function:

Plot[{Sin@x, Cos@x}, {x, 0, 4π},
  PlotStyle -> {Red, Blue}]

To plot the curves using different ColorFunctions, you can manually combine the plots:

Show[
 Plot[Sin@x, {x, 0, 4 \[Pi]},
  ColorFunction -> ({x, y} \[Function] Opacity[y, Red])],
 Plot[Cos@x, {x, 0, 4 \[Pi]},
  ColorFunction -> ({x, y} \[Function] Opacity[y, Blue])]
 ]

But if you try to combine them into one Plot[] expression, it doesn't work:

Plot[{Sin@x, Cos@x}, {x, 0, 4 \[Pi]},
 ColorFunction -> {({x, y} \[Function] 
     Opacity[y, Red]), ({x, y} \[Function] Opacity[y, Blue])}]

How can you easily plot multiple curves, specifying the ColorFunction to use for each?

Answer 1

To my knowledge, as soon as you specify a ColorFunction, every point {x,y} no matter to which function it belongs is colorized by the same function.

If you want to achieve this behavior without modifying built-in functions, you could use the UpValues of an arbitrary symbol, for instance MultiColorFunction. With this, you specify how a plot-command has to be divided into several calls which are then combined with Show. Luckily, we have to do this only once for all plot-commands (I use here only Plot and Plot3D)

MultiColorFunction /: (h : (Plot | Plot3D))[{fs__}, before___,
   MultiColorFunction[cf__], after___] := 
 Show[h[#1, before, ColorFunction -> #2, after] & @@@ 
   Transpose[{{fs}, {cf}}]]

Now you can simply call

Plot[{Sin@x, Cos@x}, {x, 0, 4 \[Pi]}, 
  MultiColorFunction["Rainbow", "Pastel"], PlotStyle -> Thick]

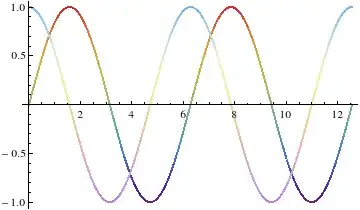
and it works similar for Plot3D

Plot3D[{Sin[x y], Cos[x]}, {x, 0, 3}, {y, 0, 3}, 
 MultiColorFunction[Function[{x, y, z}, RGBColor[x, y, 0.]], "Pastel"]]

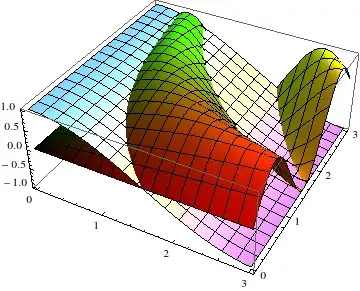
Further notes

Someone might say that when this works, why don't we use TagSet to make it possible to input this as e.g.

Plot[{Sin@x, Cos@x}, {x, 0, 4 \[Pi]}, MultiColorFunction -> {"Rainbow", "Pastel"}]

without actually defining a new option MultiColorFunction. The reason is simple, TagSet only works when the symbol we want to set is in the outer two levels. Therefore, while this

g /: f[g[h[x]]] := "blub"

works, this

h /: f[g[h[x]]] := "blub"

is not possible. Our Plot construct would have the form

Plot[....,Rule[MultiColorFunction,...],..]

so it would be equivalent to h of the example. There is of course an alternative. The last reachable level is the one of Rule but we don't want to change a built-in function. But what, if we don't use the normal Rule but a symbol which only looks like a rule-arrow? Let's try it. A quick check brings up \[RightArrow] which has no built-in meaning and looks perfect. Do you see the difference?

You can input this arrow with EscSpace->Esc and it gets automatically transformed into RightArrow[x,y].

RightArrow /: (h : (Plot | Plot3D))[{fs__}, before___,
     RightArrow[ColorFunction, {cf__}], after___] := 
  Show[h[#1, before, ColorFunction -> #2, after] & @@@ 
      Transpose[{{fs}, {cf}}]]

Plot[{Sin@x, Cos@x}, {x, 0, 4 \[Pi]}, 
  ColorFunction\[RightArrow]{"Rainbow", "Pastel"}, PlotStyle ->Thick]

Answer 2

I do not think this is possible. What happens is that both functions, in your case Sin and Cos will use the same ColorFunction and there is no way inside the ColorFunction to know which one is being called for at each time. (Unless your functions have some specific boundaries to them, that you check for inside the ColorFunction).

I did this little experiment to show this. 2 small lists listA and listB, one has 3 points, and one has 2 points. Then used ListPlot and used ColorFunction. By changing the numbers of points, and the values, one would see that ColorFunction is being called for each function, one by one.

Inside the ColorFunction a counter is used, and the point is printed. One can see that the listA is processed, followed by the 'listB, in order. i.e for each point,ColorFunction` is evaluated. It does not matter if the point is coming from the first or the second list.

i = 0;
listA =  {{0, 0}, {1, 1}, {2, 2}};
listB =  {{0, 0}, {1, 1}};

ListPlot[{listA, listB},
 ColorFunction -> Function[{x, y}, i++; Print[{i, x, y}]]
 ]

this prints

(The actual values do not match the values in the lists, due to scaling. These are coordinates into the plot window itself). But the point is, unless you know more information about each function, I do not see how to you can do what you want.

If you do know the number of points being used by each function to plot it, then you can add an If statement inside the ColorFunction to use different color based on this test.

As follows

i = 0;
listA = Table[RandomReal[], {100}];
listB = Table[RandomReal[], {30}];

ListPlot[{listA, listB},
 ColorFunction -> Function[{x, y}, If[++i <= Length[listA], Red, Blue]]
 ]

The above would require you knowing this information. This was easy for ListPlot since one knows how many points there are for each list. For non-discrete functions like Sin and Cos in your example, you'd have to first sample them yourself, then find the length of the lists generated, then use the above trick, as follows

sin = Table[{x, Sin[x]}, {x, 0, 4 Pi, .01}];
cos = Table[{x, Cos[x]}, {x, 0, 4 Pi, .01}];
i = 0;

ListLinePlot[{sin, cos},

 ColorFunction -> Function[{x, y},
   If[ ++i <= Length[sin], 
       Opacity[y, Red], 
       Opacity[y, Blue]
      ] 
  ]
 ]

Answer 3

A dirty hack that works quite well is the following:

Plot[{f1[x], f2[x]}, {x, -1, 1}, ColorFunctionScaling -> False, ColorFunction -> Function[{x, y}, If[Abs[y - f1[x]] < 10^-3, Blue, Red]]]

and you can replace Blue and Red with the ColorFunction for the first and second function, respectively.