Matching (y/x)^u terms wherever the appear in an expression

Question

Mathematica keeps rewriting expressions, so it is hard to figure what pattern to use.

I am trying to replace all occurrences of $\frac{y}{x}$ by $t$, but Mathematica re-writes $\frac{1}{\left(\frac{y}{x}\right)}$ to $\frac{x}{y}$ so pattern y/x fails sometimes depending on if it is in the numerator or denominator.

So switched to using at FullForm and checking for all combinations. But that also does not work, and I am sure I will miss some cases.

Here is an example

ClearAll[t, x, y]
expr = (y/x)^2;
FullForm[expr]

Gives

 Times[Power[x,-2], Power[y,2]]

So why does the below not match?

 expr/.Times[Power[x,-(any0_.)], Power[y,any0_.]] :>  t^any0

I am literally writing the same exact full form! But I changed the power to be anything. So in this case any0_. should match the 2, right? But it does not:

It turned out removing the minus sign before any0 above made it work, but I had to give the other power a different pattern name

   expr/.Times[Power[x, any0_.], Power[y, any1_.]] :>  t^any0

But that is not what I want. It should be $t^2$, I want the same pattern/power on both, but one with a minus sign to match. It looks like a when there is a minus sign there is a problem.

The main problem is really this: How do I change all (y/x)s anywhere in the expression to t so (y/x)^3 will change to t^3 as example?

The problem is also that Mathematica rewrites the expression internally so it is hard to know what pattern to use. What I am looking at is not what it is internally.

I even used the excellent function by Carl Woll:

getPatterns[expr_, pat_] := Last@Reap[expr /. a : pat :> Sow[a], _, Sequence @@ #2 &];
getPatterns[(y/x)^2, (y/x)^any_.]

But that did not pick this due to the re-writing.

 {}

I can't use HoldForm either on these things. Any idea how to do this which will work all the time?

Examples to test with

---

expr = (1 + 2 (y^2/x^2))/(2 (y/x))

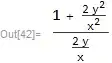
This should be transformed to $\frac{1+ 2 t^2}{2 t}$

 expr = y/x + Sqrt[1 + (y/x)^2]

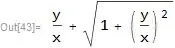
It should be transformed to $t+\sqrt{1+t^2}$

Note: It is not required that the pattern transforms things like y^4/x^3 to y t^3. It can be assumed that y/x always shows with same power. But if the transformation can handle this general case, it will be even better, but not required.

Answer 1

At least one of the problems you are encountering is that -2 and -x do not share the same structure:

{-2, -x} // FullForm

List[-2, Times[-1, x]]

You can not destructure -2 using patterns. You can check numerically however:

(y/x)^2 /. x^a_. y^b_. /; b == -a :> t^b

t^2

Remember also that a matched expression is not further replaced, so you may need ReplaceRepeated. Applied to your examples:

(1 + 2 (y^2/x^2))/(2 (y/x)) //. x^a_. y^b_. /; b == -a :> t^b

y/x + Sqrt[1 + (y/x)^2] //. x^a_. y^b_. /; b == -a :> t^b

(1 + 2 t^2)/(2 t)
t + Sqrt[1 + t^2]

---

A second potential problem is operating on a manually entered held form such as HoldForm[(1 + 2 (y^2/x^2))/(2 (y/x))] without realizing that this can have a very different internal form compared to an evaluated expression. Compare:

foo = HoldForm[(1 + 2 (y^2/x^2))/(2 (y/x))];
bar = HoldForm @@ {(1 + 2 (y^2/x^2))/(2 (y/x))};

foo // TreeForm
bar // TreeForm

---

I would be remiss not to mention that general algebraic manipulation should not be done with pattern matching if at all avoidable. See for example Replacing composite variables by a single variable and be aware of:

• Can I simplify an expression into form which uses my own definitions?

---

Other things to be aware of:

• More general pattern fails to match everything the more specific pattern does.
• Pattern matching on Orderless functions inside Hold

Answer 2

A simple solution: replace y with t x, and if there are any cases of t x hanging around with the x not cancelling, replace them with y.

(expression /. {y -> t x}) /. t x -> y

Testing it on some examples:

((1 + 2 (y^2/x^2))/(2 (y/x)) /. {y -> t x}) /. t x -> y
(y/5 /. {y -> t x}) /. t x -> y
(x/y /. {y -> t x}) /. t x -> y
(y/x + Sqrt[1 + (y/x)^2] /. {y -> t x}) /. t x -> y

(1 + 2 t^2)/(2 t)

y/5

1/t

t + Sqrt[1 + t^2]

I would imagine that this is unlikely to be very robust. But I haven't tested on any convoluted examples.

Edit: To deal with the xs left at the end, just replace them all with y/t

r[expr_] := expr /. {y -> t x} /. {t x -> y} /. {x -> y/t}

Then, in addition to the above examples, we get

r[(y/x)*y]
r[y^4/x^3]

t y

t^3 y

Answer 3

I know, this is not really the answer to your question. But at least in this specific problem, this helps:

expr /. {y -> t x}

Next try:

r = {
   Times[z___, Power[x, k_], Power[y, l_], w___] :> If[k == -l,
     Times[z, Power[t, l], w],
     Times[z, Power[x, k], Power[y, l], w]
     ],
   Times[z___, x, Power[y, -1], w___] :> Times[z, 1/t, w],
   Times[z___, Power[x, -1], y, w___] :> Times[z, t, w]
   };

x/y //. r
y^2/x^2 //. r
y^3/x^2 //. r
(1 + 2 (y^2/x^2))/(2 (y/x)) //. r
y/x + Sqrt[1 + (y/x)^2] //. r

(* 1/t *)
(* t^2 *)
(* y^3/x^2 *)
(* (1 + 2 t^2)/(2 t) *)
(* t + Sqrt[1 + t^2] *)

The second branch of the If statement can be used to further elaborate on the third example. But admittedly, this is starting to get complicated...