I am back learning pattern matching in Mathematica, which I am not good at.
An input is a mathematica expression, and I need to simply get a list of all the sub-expressions inside this expression of the pattern (any0_. Exp[any1_. c + any2_.]) anywhere in the expression.
c above is the literal symbol. All others are patterns.
For example, the above pattern will match $e^{c +x}$ or $4 e^{5 c+ x}$ and so on. So I tried it and it works, except when the input expression contains a single Exp[...]
case 1, works
ClearAll[x,y,c]
expr=x y +4 Exp[c + y]+5 Sin[x]+Exp[c + x]
Cases[expr,(any0_. Exp[any1_. c + any2_.])]

case 2, works
expr=x y +4 Exp[c + y]+5 Sin[x]
Cases[expr,(any0_. Exp[any1_. c + any2_.])]

case 3, do not work
expr=4 Exp[c + y]
Cases[expr,(any0_. Exp[any1_. c + any2_.])]

the 4 was dropped out in the above. And when there is a single Exp it does not work at all
case 4, do not work
expr=Exp[c + y]
Cases[expr,(any0_. Exp[any1_. c + any2_.])]

I can handle these last two special cases by forcing the input to be a list
expr=Exp[c + y]
Cases[{expr},(any0_. Exp[any1_. c + any2_.])]

But if I do the above, then the first two cases now fail. So I changed the test to be as follows
If[Head[expr] === Plus,
Cases[expr, (any0_. Exp[any1_. c + any2_.])]
,
Cases[{expr}, (any0_. Exp[any1_. c + any2_.])]
]
And now the above works for all of 4 cases. (But I am not sure if it will fail for some cases I have not thought about as I only check for Plus head)
My question is, is the above a correct way to do all of this, or is there a better and canonical way to handle this in Mathematica?
Update: Thanks to all the answers. But I also need it to work for division. As in this new case
case 5
expr = Exp[c + x]/(3 + Exp[3*c + x]);
So in the above, it should find Exp[c + x] and Exp[3*c + x] separately. The whole idea, is that I want to rewrite any subexpression Exp[any1_*c + any2_] as c*Exp[any2]
I did say in the original question above anywhere in the expression but I did not put the above case in there and I was just now testing the answers given and noticed this problem.
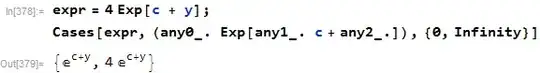
 and using
and using 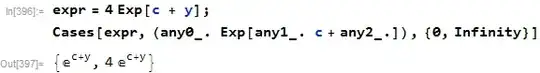 I am looking for one method that will work for all cases. But thanks for the input.
I am looking for one method that will work for all cases. But thanks for the input.
Cases[expr, (any0_. Exp[any1_. c + any2_.]), {0, Infinity}]? – kglr Jul 19 '17 at 22:074 Exp[c + y], it returned{E^(c+y),4 E^(c+y)}and I only wanted4 E^(c+y)? screen shotCases[expr, (any0_. Exp[any1_. c + any2_.]), {0}]gives a single hit. – kglr Jul 19 '17 at 22:13expr = x y + 4 Exp[c + y] + 5 Sin[x]; Cases[expr, (any0_. Exp[any1_. c + any2_.]), {0}]gives empty list.4 Exp[c + y]will have two matches for levelspec{0,1}and one for levelspec0. With yourIf[...]approach you are just adding one more level to input expr (hence default levelspec 1 kicks in). In general the pattern in the second argument, in addition to being inside an expression with anyHead, can be at arbitrary depth (considery + foo[bar[4 Exp[c=y]]for example). – kglr Jul 19 '17 at 22:33(any0_. Exp[any1_. c + any2_.])anywhere in the expression. This will be inside a black box function that user calls with an expression. You say I need to specify the level. But how? I do not know what the expression will be like. Are you saying in Mathematica it is not possible to write such a general pattern matching? – Nasser Jul 19 '17 at 22:43Cases, afaik you need{0, Infinity}as the third argument ofCases. But this returns 2 hits for4 Exp[c + y]and you only want4 E^(c+y)althoughE^(c+y)is a perfectly legitimate occurrence of your pattern inside4 Exp[c + y]. If you have a criterion in mind (that is totally different from what levelspecs can express) that determines why only4 Exp[c + y]and notExp[c + y]matches(any0_. Exp[any1_. c + any2_.])inexpr =4 Exp[c + y], ... – kglr Jul 19 '17 at 22:58