Simultaneous minimisation of chi-square

Question

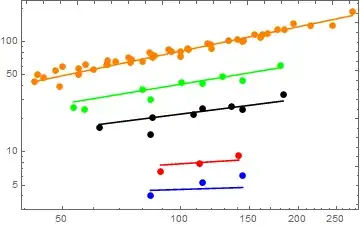
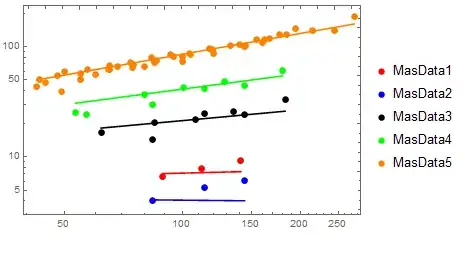
I have a series of data sets with which I would like to fit a model function to simultaneously. In each data set, I have coordinates $\left\{x,y\right\}$ and an error bar for $y$. The data sets are

MasData1 = {{{89, 6.7}, ErrorBar[1.272]}, {{112, 7.9}, ErrorBar[1.220]}, {{141, 9.3},ErrorBar[1.697]}} 

MasData2 = {{{83.9, 4.04}, ErrorBar[0.7754]}, {{114.1, 5.29},ErrorBar[1.086]}, {{144.2, 6.1},ErrorBar[1.681]}} 

MasData3 = {{{62, 16.6}, ErrorBar[2.6172]}, {{85, 20.7},ErrorBar[3.0809]}, {{108, 21.9}, ErrorBar[3.0647]}, {{135, 25.8},ErrorBar[3.9115]}, {{183, 33.2}, ErrorBar[5.993]}, {{83.9, 14.5},ErrorBar[2.772]}, {{114.1, 24.7}, ErrorBar[4.5875]}, {{144.2, 24.1},ErrorBar[6.5756]}} 

MasData4 = {{{53.3, 25.1}, ErrorBar[3.5489]}, {{83.9, 30},ErrorBar[4.309]}, {{114.1, 41.5}, ErrorBar[6.1404]}, {{144.2, 45},ErrorBar[9.6243]}, {{57, 24.4}, ErrorBar[3.6056]}, {{80, 36.7},ErrorBar[7.9925]}, {{101, 43}, ErrorBar[6.6138]}, {{128, 48.8},ErrorBar[9.1001]}, {{180, 61.1},ErrorBar[10.5575]}}

MasData5 = {{{44.8, 47.5}, ErrorBar[4.0]}, {{54.8, 50.1},ErrorBar[4.2]}, {{64.8,  61.7}, ErrorBar[5.1]}, {{74.8, 64.8},ErrorBar[5.5]}, {{84.9, 75}, ErrorBar[6.2]}, {{94.9, 81.2},ErrorBar[6.7]}, {{104.9, 85.3}, ErrorBar[7.1]}, {{119.5, 94.5},ErrorBar[7.5]}, {{144.1, 101.5}, ErrorBar[8.3]}, {{144.9, 101.9},ErrorBar[10.9]}, {{162.5, 117.8}, ErrorBar[12.8]}, {{177.3, 130.2}, ErrorBar[13.4]}, {{194.8, 147.7}, ErrorBar[17.1]}, {{60, 55.8},ErrorBar[4.838]}, {{80, 66.6}, ErrorBar[7.280]}, {{100, 73.4},ErrorBar[6.426]}, {{120, 86.7}, ErrorBar[7.245]}, {{140, 104},ErrorBar[12.083]}, {{160, 110}, ErrorBar[16.279]}, {{42.5, 43.8},ErrorBar[3.482]}, {{55, 57.2}, ErrorBar[3.980]}, {{65, 62.5},ErrorBar[4.614]}, {{75, 68.9}, ErrorBar[5.197]}, {{85, 72.1},ErrorBar[5.523]}, {{100, 81.9}, ErrorBar[5.368]}, {{117.5, 95.7},ErrorBar[6.277]}, {{132.5, 103.9},ErrorBar[6.912]}, {{155, 115.7}, ErrorBar[7.920]}, {{185, 129.1}, ErrorBar[9.192]}, {{215, 141.7}, ErrorBar[10.666]}, {{245, 140.3}, ErrorBar[14.526]}, {{275, 189}, ErrorBar[24.274]}, {{49, 39.2},ErrorBar[10]}, {{86, 75.7}, ErrorBar[14.414]}, {{167, 118},ErrorBar[22.828]}, {{43.2, 50.7}, ErrorBar[1.5]}, {{50, 59.5},ErrorBar[1.4]}, {{57.3, 61.8}, ErrorBar[1.9]}, {{65.3, 67.6},ErrorBar[1.7]}, {{73.9, 72.4}, ErrorBar[1.9]}, {{83.2, 79.9},ErrorBar[2.3]}, {{93.3, 84.4}, ErrorBar[2.1]}, {{104.3, 86.7},ErrorBar[2.7]}, {{47.9, 55.4}, ErrorBar[2.1]}, {{68.4, 66.4},ErrorBar[2.9]}}

Now, I wish to fit the model function

f1[x_] = NN*x^(-a-b*Log[q/0.45])

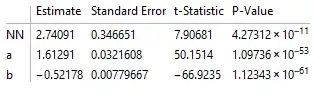
to the data sets simultaneously. Each data set corresponds to a particular value of q. In MasData1 q = 6.4025, in MasData2 q = 8.0025, in MasData3 q=4.1525, in MasData4 q=3.2025 and in MasData5 q = 2.4025. So for a given data set, the model function to be fitted is a function of $NN, a,b$ and $x$. The set $\left\{NN,a,b\right\}$ constitutes the parameters which I would like to find a best estimate for through the minimisation of a $\chi^2$

My attempt so far is to find a chi-square function for each data set but I am not sure how to minimise them all simultaneously.

 f1[x_] = NN*x^(-a - b*Log[y1/0.45]) /. y1 -> 6.4025

 chisq1 = Sum[((MasData1[[k]][[1]][[2]] - f1[MasData1[[k]][[1]][[1]]])/MasData1[[k]][[2]][[1]])^2, {k, 1, Length[MasData1]}]

 f2[x_] = NN*x^(-a - b*Log[y2/0.45]) /. y2 -> 8.0025

 chisq2 = Sum[((MasData2[[k]][[1]][[2]] - f2[MasData2[[k]][[1]][[1]]])/MasData2[[k]][[2]][[1]])^2, {k, 1, Length[MasData2]}]

 f3[x_] = NN*x^(-a - b*Log[y3/0.45]) /. y3 -> 4.1525

 chisq3 = Sum[((MasData3[[k]][[1]][[2]] - f3[MasData3[[k]][[1]][[1]]])/MasData3[[k]][[2]][[1]])^2/5, {k, 1, Length[MasData3]}]

 f4[x_] = NN*x^(-a - b*Log[y4/0.45]) /. y4 -> 3.2025

 chisq4 = Sum[((MasData4[[k]][[1]][[2]] - f4[MasData4[[k]][[1]][[1]]])/MasData4[[k]][[2]][[1]])^2/6, {k, 1, Length[MasData4]}]

 f5[x_] = NN*x^(-a - b*Log[y5/0.45]) /. y5 -> 2.4025

 chisq5 = Sum[((MasData5[[k]][[1]][[2]] - f5[MasData5[[k]][[1]][[1]]])/MasData5[[k]][[2]][[1]])^2/42, {k, 1, Length[MasData5]}]

Then I would like to find one set of values for NN,a,b that are the best estimate parameters of the model function describing all the data points. How to do this in mathematica?

Thanks!

Also identical to https://mathematica.stackexchange.com/questions/152886/chisquare-fit-to-multiple-data-sets but the above question has more details and more datasets. — JimB, Aug 08 '17 at 14:13

JimB · Answer 1 · 2017-08-09T14:48:12.683

This appears to be a straightforward regression problem. (If there is some reference to fitting regression problems with a $\chi^2$, please give a reference.)

First make a single dataset with the q values included and the ErrorBar's tossed. (The ErrorBar's in this case just aren't needed.)

qq = {6.4025, 8.0025, 4.1525, 3.2025, 2.4025};
d1 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[1]], Length[MasData1]]}], MasData1[[All, 1]]}}];
d2 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[2]], Length[MasData2]]}], MasData2[[All, 1]]}}];
d3 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[3]], Length[MasData3]]}], MasData3[[All, 1]]}}];
d4 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[4]], Length[MasData4]]}], MasData4[[All, 1]]}}];
d5 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[5]], Length[MasData5]]}], MasData5[[All, 1]]}}];
data = Join[d1, d2, d3, d4, d5];

Take the log of the dependent variable:

data[[All, 3]] = Log[data[[All, 3]]];

Fit the model:

nlm = NonlinearModelFit[data, Log[NN] + (a + b Log[q/0.45]) Log[x], {NN, a, b}, {q, x}];
sol = nlm["BestFitParameters"]
{NN -> 2.74091, a -> 1.61291, b -> -0.52178}

Plot the results:

Show[ListLogLogPlot[{d1[[All, {2, 3}]], d2[[All, {2, 3}]],
   d3[[All, {2, 3}]], d4[[All, {2, 3}]], d5[[All, {2, 3}]]},
  PlotStyle -> {{Red, PointSize[0.02]}, {Blue, PointSize[0.02]},
    {Black, PointSize[0.02]}, {Green, PointSize[0.02]}, {Orange, PointSize[0.02]}},
  Frame -> True,
  PlotLegends -> {"MasData1", "MasData2", "MasData3", "MasData4", "MasData5"}],
 LogLogPlot[Exp[nlm[qq[[1]], x]], {x, Min[d1[[All, 2]]], Max[d1[[All, 2]]]}, PlotStyle -> Red],
 LogLogPlot[Exp[nlm[qq[[2]], x]], {x, Min[d2[[All, 2]]], Max[d2[[All, 2]]]}, PlotStyle -> Blue],
 LogLogPlot[Exp[nlm[qq[[3]], x]], {x, Min[d3[[All, 2]]], Max[d3[[All, 2]]]}, PlotStyle -> Black],
 LogLogPlot[Exp[nlm[qq[[4]], x]], {x, Min[d4[[All, 2]]], Max[d4[[All, 2]]]}, PlotStyle -> Green],
 LogLogPlot[Exp[nlm[qq[[5]], x]], {x, Min[d5[[All, 2]]], Max[d5[[All, 2]]]}, PlotStyle -> Orange]]

2nd update Using the standard regression approach one can obtain measures of precision for the parameter estimates. ("An estimate without an associated measure of precision is at best of unknown value.")

nlm["ParameterTable"]

nlm["CorrelationMatrix"] // MatrixForm

$$\left( \begin{array}{ccc} 1. & -0.887054 & 0.0844225 \\ -0.887054 & 1. & -0.52751 \\ 0.0844225 & -0.52751 & 1. \\ \end{array} \right)$$

Update

Your question asks for how to estimate NN, a, and b by minimizing a $\chi^2$ function using the values from the error bars. I really don't recommend that not only because it is unnecessary for a standard regression but you also don't get any associated measures of precision for the estimated coefficients (unless you went further and performed some sort of bootstrap process). But in any event, here is how you'd do it.

First create a dataset containing everything:

qq = {6.4025, 8.0025, 4.1525, 3.2025, 2.4025};
d1 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[1]], Length[MasData1]]}], 
     Flatten[#] & /@ (MasData1 /. ErrorBar -> List)}}];
d2 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[2]], Length[MasData2]]}], 
     Flatten[#] & /@ (MasData2 /. ErrorBar -> List)}}];
d3 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[3]], Length[MasData3]]}], 
     Flatten[#] & /@ (MasData3 /. ErrorBar -> List)}}];
d4 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[4]], Length[MasData4]]}], 
     Flatten[#] & /@ (MasData4 /. ErrorBar -> List)}}];
d5 = ArrayFlatten[{{Transpose[{ConstantArray[qq[[5]], Length[MasData5]]}], 
     Flatten[#] & /@ (MasData5 /. ErrorBar -> List)}}];
data = Join[d1, d2, d3, d4, d5];

Define the $\chi^2$ statistic and find the values of the parameters that minimize the $\chi^2$ statistic.

f = Total[((data[[All, 3]] - NN data[[All, 2]]^(a + b Log[data[[All, 1]]/0.45]))/data[[All, 4]])^2];
min\[chi]2 = FindMinimum[{f, NN > 0 }, {{NN, 2.7}, {a, 1.6}, {b, -.5}}]
(* {NN -> 4.77618, a -> 1.55039, b -> -0.551016} *)

The resulting values are a bit different from before.

Here is a plot showing the fit:

Show[ListLogLogPlot[{d1[[All, {2, 3}]], d2[[All, {2, 3}]],
   d3[[All, {2, 3}]], d4[[All, {2, 3}]], d5[[All, {2, 3}]]},
  PlotStyle -> {{Red, PointSize[0.02]}, {Blue, PointSize[0.02]},
    {Black, PointSize[0.02]}, {Green, PointSize[0.02]}, {Orange, 
     PointSize[0.02]}},
  Frame -> True,
  PlotLegends -> {"MasData1", "MasData2", "MasData3", "MasData4", 
    "MasData5"}],
 LogLogPlot[NN x^(a + b Log[qq[[1]]/0.45]) /. min\[Chi]2[[2]],
{x, Min[d1[[All, 2]]], Max[d1[[All, 2]]]}, PlotStyle -> Red],
     LogLogPlot[NN x^(a + b Log[qq[[2]]/0.45]) /. min\[Chi]2[[2]],
{x, Min[d2[[All, 2]]], Max[d2[[All, 2]]]}, PlotStyle -> Blue],
     LogLogPlot[NN x^(a + b Log[qq[[3]]/0.45]) /. min\[Chi]2[[2]],
{x, Min[d3[[All, 2]]], Max[d3[[All, 2]]]}, PlotStyle -> Black],
     LogLogPlot[NN x^(a + b Log[qq[[4]]/0.45]) /. min\[Chi]2[[2]],
{x, Min[d4[[All, 2]]], Max[d4[[All, 2]]]}, PlotStyle -> Green],
     LogLogPlot[NN x^(a + b Log[qq[[5]]/0.45]) /. min\[Chi]2[[2]],
{x, Min[d5[[All, 2]]], Max[d5[[All, 2]]]}, PlotStyle -> Orange]]

The fit is not so good for MasData1 and MasData2. An there are no automatic estimates of precision.

Thanks again! I just wonder what is the difference between the best fit parameters obtained through minimisation of a chi square function from those you obtained above? And is there not an analysis one can do using the error bars? This would perhaps involve a minimisation procedure where we would like to find the best fit parameters for a fit that lies between the various error bands +1 — CAF, Aug 08 '17 at 17:03
There is a definite increase in the size of the error bar with increasing values of the dependent variable. So at first sight that ought to be incorporated. However, that increase looks pretty linear which would likely "disappear" once the analysis is performed on the log scale of the dependent variable. In addition, those error bars don't include any measure of lack of fit to the underlying function and it's unclear what statistical properties the estimates would have if the $\chi^2$ statistic would be minimized. If I have time in the next day or so, I'll elaborate more. — JimB, Aug 08 '17 at 17:12
Many thanks for the update - Regarding the automatic estimates of precision between $NN,a,b$ do you mean that in the way without minimisation of the $\chi^2$ statistic, one could just write nlm["CorrelationMatrix"] and this would generate the correlation matrix in the space of parameters? — CAF, Aug 09 '17 at 10:28
Added a few sentences about measures of precision from the regression approach. — JimB, Aug 09 '17 at 14:48
I see thanks, so I guess a chi square is only useful if one assumes the data points and their errors are Gaussian distributed and/or if you want to obtain a measure of goodness of fit via the $\chi^2$ per degree of freedom less than or around one. I couldn't see something analogous to the latter in the nonlinearfitmodel procedure , is that correct? — CAF, Aug 09 '17 at 16:16
If "goodness of fit" is what you didn't see in NonlinearModelFit, I would recommend looking at the square root of "EstimatedVariance" as that value is in the same units as the predicted variable which means you can apply your subject matter knowledge to make an assessment. The $\chi^2$ statistic you used is unitless, devoid of subject matter interpretation, and depends not only on the goodness of fit but also on sample size (i.e., those with bigger budgets will obtain larger $\chi^2$ values). But such issues would be better addressed at the CrossValidated site. — JimB, Aug 09 '17 at 16:35

Simultaneous minimisation of chi-square

1 Answers1

Linked