0

I have often to do with experimental data (with a certain length and given sampling frequency) where I obtain trajetories of moving objects in 2d. Then I am interested to find out what the corresponding freqency spectrum is, if the objects are excited by external sources and what the resonance frequencies and amplitudes are.

To do that I could use the example which I translated from here.

Example:

I produce data containing a 50 Hz sinusoid of amplitude 0.7 and a 120 Hz sinusoid of amplitude 1.

fs = 1000;(*Sampling frequency*)
tp = 1/fs;(*Sampling period*)
l = 1500;(*Length of signal*)

t = Range[0, l - 1, 1]*tp;(*Time vector*)

x = 0.7*Sin[2*Pi*50*t] + Sin[2*Pi*120*t];

ListLinePlot[Transpose[{t[[1 ;; 50]], x[[1 ;; 50]]}], 
  Frame -> True, FrameLabel -> {"t", "x (t)"}]

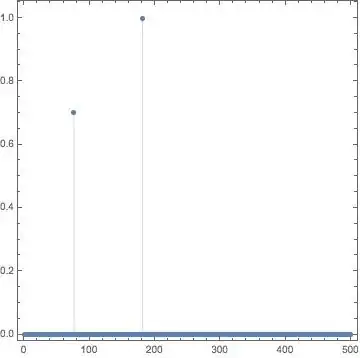
enter image description here

Now I want to calculate the frequency spectrum, which should show two peaks at 50 Hz with amplitude 0.7 and at 120 Hz with amplitude 1.

f = fs*Range[0, l/2, 1]/l;

y = Fourier[x, FourierParameters -> {1, -1}];

p2 = Abs[y/l];

p1 = p2[[1 ;; l/2 + 1]];

p1[[2 ;; Length@p1 - 1]] = 2*p1[[2 ;; Length@p1 - 1]];

ListLinePlot[Transpose[{f, p1}], Frame -> True, 
  FrameLabel -> {"f (Hz)", "Abs[p1(f)]"}, PlotRange -> Full]

So far, I can reproduce what is shown by Matlab with their example code.

enter image description here

Question: What would be a Matematica-like solution for my problem?

I have seen that Mathematica provides the function Periodogram. With that I tried the following:

plot = Periodogram[x, FourierParameters -> {-1, 1}, SampleRate -> fs, 
   Frame -> True, FrameLabel -> {"f (Hz)", "Abs[p1(f)]"}, 
   PlotRange -> Full, ScalingFunctions -> "Absolute"]

enter image description here

As one can see: the frequencies are found, but the amplitudes are not correct.

Once I would find the correct amplitudes with Periodogram I could use a solution from Mr.Wizard to retrieve the data lists of the frequency and amplitude.

data = Select[Rectangle @@ (PlotRange[plot]\[Transpose]) // RegionMember] /@ 
  Cases[Normal@plot, _Point | _Line, -1][[All, 1]];

ListLinePlot[data, Frame -> True, FrameLabel -> {"f (Hz)", "Abs[p1(f)]"},
  PlotRange -> Full]

enter image description here

mrz
  • 11,686
  • 2
  • 25
  • 81
  • 1
    The amplitudes shown in Periodogram depend on the window function. If you know which one matlab uses you could use the same in Mathematica. But for your original problem i think the manual route via Fourier is a good way to go. – Thies Heidecke Nov 17 '17 at 14:03
  • 1
    If you are after amplitudes I would stick to Fourier and choose appropriate FourierParameters. The answer here may be of some help. If I have time I will post a full answer. – Hugh Nov 17 '17 at 14:40
  • @Hugh: Thanks a lot for the link. – mrz Nov 17 '17 at 15:02
  • 1
    Prony's method will recover frequencies and amplitudes. Check here for implementation code. When I change a few variable names from that code to match the definitions above I get the desired values. – Daniel Lichtblau Nov 17 '17 at 16:01
  • 1
    @Daniel Lichtblau: Thank you very much for your mentioned link and also to the link to the discussion on Wolfram Community: http://community.wolfram.com/groups/-/m/t/528474?p_p_auth=33hR9Jgo. – mrz Nov 17 '17 at 16:30

1 Answers1

2

Use the Abs for the Fourier transform of the data (Fourier), and do not forget to normalise:

absft = Abs@Fourier[x] // Chop; 
ListPlot[absft[[1 ;; Length[absft]/3]]/Max[absft], PlotRange -> All, 
Filling -> Bottom, AspectRatio -> 1, Frame -> True, PlotStyle -> PointSize[0.015]]

enter image description here

José Antonio Díaz Navas
  • 6,103
  • 1
  • 20
  • 30