Extract data from DateListPlot, limited by PlotRange

Question

Extracting the points from a line in a ListPlot in this answer uses

points = Cases[Normal@plot, Line[pts_] :> pts, Infinity];

This works in DateListPlot (provided Joined->True) (example below, using Last to get the y-axis data only)

Clear[test,plot,points];
test={{"2010",1},{"2011",2},{"2012",3},{"2014",4},{"2015",5},{"2016",6}};
plot=DateListPlot[test,Joined->True]
points=Last/@Flatten[Cases[Normal@plot,Line[pts_]:>pts,Infinity],1]

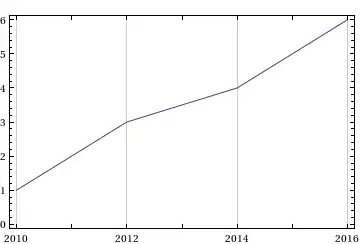
enter image description here

(*OUTPUT
{1.,2.,3.,4.,5.,6.}

However, when the plot is limited by PlotRange using date values (lower plot), the function returns the entire list of points.

plot2=DateListPlot[test,Joined->True,PlotRange->{{"2012","2015"},{0,6}}]
points2=Last/@Flatten[Cases[Normal@plot2,Line[pts_]:>pts,Infinity],1]

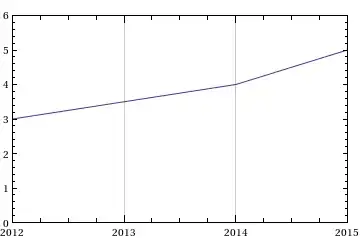
enter image description here

(*OUTPUT
{1.,2.,3.,4.,5.,6.}

Is there a function, like points which can return only the points displayed on the plot in DateListPlot under 'PlotRange` ?

You can just use Select on the result with conditions similar to those in PlotRange. — Kuba, Jun 09 '14 at 23:27
@Kuba Appreciated. Pickett is along those lines too and delves into the plot function to retrieve the bounds — PlaysDice, Jun 09 '14 at 23:41
@rasher Thanks. The linked answer is a serious Module indeed! — PlaysDice, Jun 09 '14 at 23:51

score 3 · Accepted Answer · answered Jun 09 '14 at 23:28

3

This should do it:

points2 = 
 With[{range = Part[PlotRange /. Options[plot2], 1]}, 
  Select[Flatten[Cases[Normal@plot2, Line[pts_] :> pts, Infinity], 1],
     First@range <= First@# && First@# <= Last@range &][[All, 2]]]

With plot2 as in your example:

{3., 4., 5.}

answered Jun 09 '14 at 23:28

C. E.

70,533
6
140
264

Yes! I was hoping someone could retrieve the values with Options magic. – PlaysDice Jun 09 '14 at 23:40
1

I worked through what you did. Using the Options to make a set of replace rules and PlotRange as the "target of those replace rules" is very neat. I learned something new (again). – PlaysDice Jun 10 '14 at 02:20
@PlaysDice I'm glad you liked it! :) – C. E. Jun 10 '14 at 02:27

score 2 · Answer 2 · answered Apr 18 '15 at 16:06

A variant of Pickett's answer:

using new-in-10 RegionMember
with a terse way to extract the plot range
extended to either Line or Point data
written as a reusable function

Code:

inrangeData[gr_Graphics] := 
  Select[Rectangle @@ (PlotRange[gr]\[Transpose]) // RegionMember] /@ 
    Cases[Normal @ gr, _Point | _Line, -1][[All, 1]]

Test:

inrangeData[plot2]

{{{3.53436*10^9, 3.}, {3.59752*10^9, 4.}, {3.62906*10^9, 5.}}}

ListPlot[Prime @ Range @ 25, PlotRange -> {20, 40}]

% // inrangeData

enter image description here

{{{9., 23.}, {10., 29.}, {11., 31.}, {12., 37.}}}

The extra bracket depth is there to allow the function to handle plots with multiple lines or sets:

ListLinePlot[
  Table[{k, PDF[BinomialDistribution[50, p], k]}, {p, {0.3, 0.5, 0.8}}, {k, 0, 50}], 
  PlotRange -> {0.08, 0.15},
  Filling -> Axis
]

% // inrangeData

enter image description here

{
 {
  {11.838, 0.08}, {11.8528, 0.08035}, {12., 0.0838297}, {13., 0.105017},
  {14., 0.118948}, {15., 0.122347}, {16., 0.1147}, {17., 0.0983144},
  {17.8527, 0.08035}, {17.8693, 0.08}
 },
 {
  {22.0685, 0.08}, {22.089, 0.08035}, {23., 0.0959617}, {24., 0.107957},
  {25., 0.112275}, {26., 0.107957}, {27., 0.0959617}, {27.911, 0.08035},
  {27.9315, 0.08}
 },
 {
  {37.1629, 0.08}, {37.1755, 0.08035}, {38., 0.103275}, {39., 0.127108},
  {40., 0.139819}, {41., 0.136409}, {42., 0.116922}, {43., 0.0870116},
  {43.2105, 0.08035}, {43.2216, 0.08}
 }
}

Extract data from DateListPlot, limited by PlotRange

2 Answers2

Linked