2

With IntegerPartitions[7], I have partitions of 7 into integers that are smaller than 6 as follows.

{5, 2}, 
{5, 1, 1}, 
{4, 3}, 
{4, 2, 1}, 
{4, 1, 1, 1}, 
{3, 3, 1}, 
{3, 2, 2}, 
{3, 2, 1, 1}, 
{3, 1, 1, 1, 1}, 
{2, 2, 2, 1}, 
{2, 2, 1, 1, 1}, 
{2, 1, 1, 1, 1, 1}, 
{1, 1, 1, 1, 1, 1, 1}

Furthermore, I want to include the permutation of each partition. For the first partition, for example, I also want to include {2, 5}.

Question

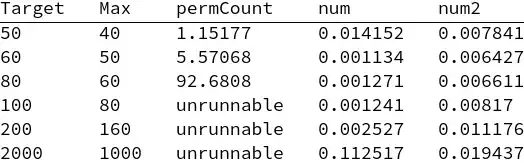
How to calculate the whole permutation of the partition of 7 given above? I don't need the list for sure, but just the length of the list.

Community
  • 1
Display Name
  • 2,009
  • 8
  • 17

2 Answers2

8

Perhaps a slightly more efficient method:

 ClearAll["Global`*"]

 num[int_,max_]:=SeriesCoefficient[(1-x)/(1-2x+x^(max+1)),{x,0,int}];

Arguments are target number and maximum allowed element in partitions.

For large cases, the following (same arguments as above) can net additional speed, depending on relative magnitudes of the target and maximum:

num2=ParallelSum[(-1)^r Binomial[#1-#2*r-1, n-1] Binomial[n, r],{n,#1},{r,0,(#1 - n)/#2}]&;

Some timing comparisons:

enter image description here

Warning: Don't even think about trying test cases of this size with extant answers, you'll probably crash the kernel or lockup your machine.

ciao
  • 25,774
  • 2
  • 58
  • 139
4

You could just apply Permutations to the partitions:

Length @ Catenate @ Map[Permutations] @ IntegerPartitions[7, 7, Range[5]]

61

update

And, a faster version that avoids computing all the permutations:

permCount[list_] := Multinomial @@ Tally[list][[All,2]]

Total @ Map[permCount] @ IntegerPartitions[7, 7, Range[5]]

61

Carl Woll
  • 130,679
  • 6
  • 243
  • 355