Most efficient way to build block / banded SparseArray

Question

I have a matrix that I generate with a procedure that looks like this:

blaMX[ptsX_Integer, ptsY_Integer] :=
  Table[
   With[
    {
     ix = 1 + Floor[(i - 1)/(ptsY)], jx = 1 + Floor[(j - 1)/(ptsY)],
     iy = Mod[i, ptsY, 1], jy = Mod[j, ptsY, 1]
     },
    If[iy != jy,
      0,
      k1[ix, jx]
      ] +
     If[ix != jx,
      0,
      k2[iy, jy]
      ]
    ],
   {i, ptsX*ptsY},
   {j, ptsX*ptsY}
   ];

where I have two square matrices k1 of dimension ptsX and k2 of dimension ptsY

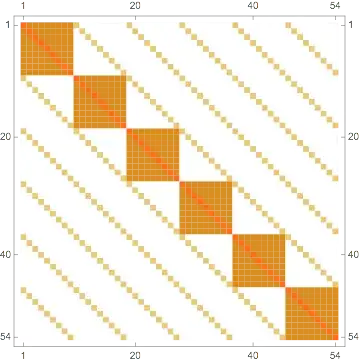
It generates a block-diagonal matrix with a bunch of block-bands. The basic structure looks like:

blaMX[6, 9] /. {_k1 -> 1, _k2 -> 2, c -> 3} // MatrixPlot

where each of those diagonal blocks is k2 duplicated:

blaMX[3, 6][[7 ;; 12, 7 ;; 12]] /. _k1 -> 0 // Grid

k2[1,1] k2[1,2] k2[1,3] k2[1,4] k2[1,5] k2[1,6]
k2[2,1] k2[2,2] k2[2,3] k2[2,4] k2[2,5] k2[2,6]
k2[3,1] k2[3,2] k2[3,3] k2[3,4] k2[3,5] k2[3,6]
k2[4,1] k2[4,2] k2[4,3] k2[4,4] k2[4,5] k2[4,6]
k2[5,1] k2[5,2] k2[5,3] k2[5,4] k2[5,5] k2[5,6]
k2[6,1] k2[6,2] k2[6,3] k2[6,4] k2[6,5] k2[6,6]

Each band is made up of blocks, as an unwrapping of k1 with the Band starting at {n+(i-1)*ptsY, n+(j-1)*ptsY} being k1[[i+1, j+1]] (essentially just using Quotient:

With[{n = 1},
  Table[
   blaMX[6, 9][[
      (i - 1)*9 + n, 
      (j - 1)*9 + n
      ]] /. _k2 -> 0,
   {i, 6},
   {j, 6}
   ]
  ] // Grid

Now, my generation procedure is wildly inefficient. I do ptsX^2 * ptsY^2 work, when I really only have ptsX * ptsY * (ptsX + ptsY - 1) (which is just 2 n^3 - n^2 if ptsX == ptsY == n) non-zero elements.

So, what is the best way to build a matrix of this form? My current version looks like:

makeKMat[k1_, k2_] :=
  With[{
    k1SparseRules =
     With[{ptsX = Length@k1, ptsY = Length@k2},
      Flatten[
       Table[
        Band[{(i - 1)*ptsY + 1, (j - 1)*ptsY + 1}, {i*ptsY, j*ptsY}] ->
         k1[[i, j]],
        {i, ptsX},
        {j, ptsX}
        ],
       1
       ]
      ],
    k2SparseRules =
     With[{ptsX = Length@k1, ptsY = Length@k2},
      {
       Band[{1, 1}] ->
        ConstantArray[k2, ptsX]
       }
      ]
    },
   With[{k3 = SparseArray[k2SparseRules]},
    SparseArray[k1SparseRules, Dimensions[k3]] + k3
    ]
   ];

And this works:

k1Pts = 6;
k2Pts = 9;
k1Test = Array[k1, {k1Pts, k1Pts}];
k2Test = Array[k2, {k2Pts, k2Pts}];
kMatTest = makeKMat[k1Test, k2Test];
kMatTest == blaMX[6, 9]

True

And is pretty fast, all considered:

k1Test2 = RandomReal[{}, {15, 15}];
k2Test2 = RandomReal[{}, {15, 15}];

{tt, mx} = makeKMat[k1Test2, k2Test2] // RepeatedTiming;
tt

0.0071

{tt2, lmx} = lazyMX[k1Test2, k2Test2] // RepeatedTiming;
tt2

0.338

But, I can't help but feel that this could be done more efficiently. Can someone propose a better way to build a block-banded SparseArray like this?

---

Some mild goal-post moving:

What if we wanted to extend this to an $N$-dimensional system? A way to implement this element-wise would be:

getCrds[i_, j_, gridDivs_] :=
  FoldList[
    With[{tot = #[[3]], new = #2},
      Append[
       Map[
        Mod[1 + Quotient[# - 1, tot], new, 1] &,
        {i, j}
        ],
       tot*new
       ]
      ] &,
    {i, j, 1},
    gridDivs
    ][[2 ;;, ;; 2]];

makeNDKMat[ks : {__List}] :=
 With[{gridDivs = Length /@ ks},
  Table[
   With[{divvy = getCrds[i, j, gridDivs]},
    Total@
     Table[
      If[AllTrue[Delete[divvy, k], Apply[Equal]],
       ks[[k, Sequence @@ divvy[[k]]]],
       0
       ],
      {k, Length@gridDivs}
      ]
    ],
   {i, Times @@ gridDivs},
   {j, Times @@ gridDivs}
   ]
  ]

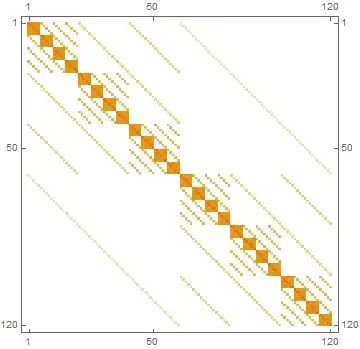
For example, in 4D this looks like:

k1T = Array[k1, {2, 2}];
k2T = Array[k2, {3, 3}];
k3T = Array[k3, {4, 4}];
k4T = Array[k4, {5, 5}];
k4DLazy = 
  makeNDKMat[{k4T, k3T, k2T, k1T}] /. {_k1 -> 1, _k2 -> 2, _k3 -> 
     3, _k4 -> 4};
k4DLazy // MatrixPlot

How could we efficiently build a sparse representation of this?

Answer 1

This is definitely faster. It took me some time to figure out the combinatorics and there might still be some potential for improvement within the compiled functions.

getColumnIndices = Compile[{{m, _Integer}, {n, _Integer}, {i, _Integer}},
   Transpose[Partition[
     Partition[
      Join[
       Table[k, {k, 1, i n}],
       Flatten[Table[Table[k, {j, 1, n}], {k, i n + 1, i n + n}]],
       Table[k, {k, i n + n + 1, m n}]
       ], {1}], {n}]],
   RuntimeAttributes -> {Listable},
   Parallelization -> True,
   CompilationTarget -> "C",
   RuntimeOptions -> "Speed"
   ];

getValues = Compile[{{k1row, _Real, 1}, {k2, _Real, 2}, {i, _Integer}},
   Block[{A},
    A = Join[
      Table[Compile`GetElement[k1row, k], {l, 1, Length[k2]}, {k, 1, i}],
      k2,
      Table[Compile`GetElement[k1row, k], {l, 1, Length[k2]}, {k, i + 2, Length[k1row]}],
      2
      ];
    Do[A[[k, k + i]] += Compile`GetElement[k1row, i + 1], {k, 1, Length[k2]}];
    A
    ],
   RuntimeAttributes -> {Listable},
   Parallelization -> True,
   CompilationTarget -> "C",
   RuntimeOptions -> "Speed"
   ];

makeKMat3[k1_, k2_] := With[{m = Length[k1], n = Length[k2]},
  SparseArray @@ {Automatic, {m n, m n}, 0, {1, {
      Range[0, (m n ) (m + n - 1), m + n - 1],
      Flatten[getColumnIndices[m, n, Range[0, m - 1]], 2]
      },
     Flatten[getValues[k1, k2, Range[0, m - 1]]]
     }}
  ]

Just to give you an idea of the timings:

m = 100;
n = 6;
k1 = RandomReal[{-1, 1}, {m, m}];
k2 = RandomReal[{-1, 1}, {n, n}];
A = makeKMat2[k1, k2]; // RepeatedTiming
B = makeKMat3[k1, k2]; // RepeatedTiming
Max[Abs[A - B]]

{0.11, Null}

{0.000481, Null}

0.

Addendum

The idea for the "higher dimensional" case is similar to the idea above. I exploit that the "ColumnIndices" of the resulting matrices (when partitioned into column indices per row) stay rectangular so that column indices from the diagonal matrices can be joined to it from the left and right. Some extra index list (diagidx) is needed for book keeping of those column indices of the blocks that belong to the diagonal entries. All in all, only operations on the nonzero values and the column indices are performed. No SparseArrays are built intermediately: Even building a SparseArray from row pointers, column indices and nonzero values has still some considerable overhead, probably because there is a consistency checker involved in the backend. That's a pitty since I know that I produce consistent data. This issue is also closely related to this post by Szabolcs.

getValues2 = Compile[{{k1row, _Real, 1}, {blockvals, _Real, 2}, {diagidx, _Integer, 1}, {i, _Integer}},
   Block[{A},
    A = Join[
      Table[Compile`GetElement[k1row, k], {l, 1, Dimensions[blockvals][[1]]}, {k, 1, i}],
      blockvals,
      Table[Compile`GetElement[k1row, k], {l, 1, Dimensions[blockvals][[1]]}, {k, i + 2, Length[k1row]}],
      2];
    Do[A[[k, Compile`GetElement[diagidx, k] + i]] += Compile`GetElement[k1row, i + 1], {k, 1, Length[blockvals]}];
    A
    ],
   RuntimeAttributes -> {Listable},
   Parallelization -> True,
   CompilationTarget -> "C",
   RuntimeOptions -> "Speed"
   ];

getColumnIndices2 = Compile[{
    {blockci, _Integer, 3}, {diagci, _Integer, 
     3}, {m, _Integer}, {n, _Integer}, {i, _Integer}
    },
   If[i > 0,
    If[i < m - 1,
     Join[diagci[[All, 1 ;; i]], blockci + i n, diagci[[All, i + 1 ;; m - 1]] + (n), 2],
     Join[diagci[[All, 1 ;; i]], blockci + i n, 2]
     ],
    Join[blockci + i n, diagci[[All, i + 1 ;; m - 1]] + (n), 2]
    ],
   RuntimeAttributes -> {Listable},
   Parallelization -> True,
   CompilationTarget -> "C",
   RuntimeOptions -> "Speed"
   ];

toSparseArrayData[b_?MatrixQ] := {
  Partition[SparseArray[b]["ColumnIndices"], Dimensions[b][[2]]],
  b,
  Dimensions[b][[2]],
  Range[Dimensions[b][[2]]]
  }

toSparseArray[X_] := 
 With[{d1 = Dimensions[X[[1]]][[1]], d2 = Dimensions[X[[1]]][[2]]},
  SparseArray @@ {Automatic, {d1, d1}, 0,
    {1, {Range[0, d1 d2, d2], Flatten[X[[1]], 1]}, Flatten[X[[2]]]}}
  ]

iteration[X_, a_] := With[{
   m = Length[a],
   blockci = X[[1]],
   blockvals = X[[2]],
   n = X[[3]],
   diagidx = X[[4]]
   },
  With[{ran = Range[0, m - 1]},
   {
    Join @@ getColumnIndices2[blockci, Transpose[Partition[Partition[Range[(m - 1) n], 1], n]], m, n, ran],
    Join @@ getValues2[a, blockvals, diagidx, ran],
    m n,
    Join @@ Outer[Plus, ran, diagidx]
    }
   ]
  ]

makeKMat3ND[ks : {__List}] := 
 toSparseArray[Fold[iteration, toSparseArrayData[ks[[1]]], Rest[ks]]]

Usage example and timing test:

SeedRandom[123];
ks = Table[RandomReal[{-1, 1}, {RandomInteger[{3, 8}]}[[{1, 1}]]], 6];
A = makeKMat2ND[Reverse@ks]; // AbsoluteTiming
B = makeKMat3ND[ks]; // AbsoluteTiming
Max[Abs[A - B]]

{24.0011, Null}

{0.038756, Null}

8.88178*10^-16

This is the sparsity pattern of the resulting matrix:

Answer 2

Not faster, but maybe easier to implement

makeKMat2[k1_, k2_] := Module[{A, m, n},
  m = Length[k1];
  n = Length[k2];
  A = Map[SparseArray[Band[{1, 1}] -> #, {n, n}, 0.] &, k1, {2}];
  With[{B = SparseArray@k2}, Do[A[[i, i]] += B, {i, 1, m}]];
  ArrayFlatten[A]
  ]

Your implementation needs about 0.0048s; mine needs 0.0051s on my machine.

(b3m2a1 comment)
Note that this has a simple extension to the N-dimensional case:

makeKMat2ND[ks : {__List}] := Fold[makeKMat2, ks]

Answer 3

This is slightly faster and certainly more compact than the uncompiled implementation in Henrik's answer:

makeKMat[k1_?SquareMatrixQ, k2_?SquareMatrixQ] := Module[{m = Length[k1], n = Length[k2]},
    KroneckerProduct[k1, IdentityMatrix[n, SparseArray]] + 
    KroneckerProduct[IdentityMatrix[m, SparseArray], k2]]

and as b3m2a1 notes, the extension can be done as

makeKMatND[ks : {__?SquareMatrixQ}] := Fold[makeKMat[#2, #1] &, ks]

Using the examples in the OP:

MatrixPlot[makeKMat[ConstantArray[1, {9, 9}], ConstantArray[2, {6, 6}]]]

AbsoluteTiming[tst =
               makeKMatND[{ConstantArray[4, {5, 5}], ConstantArray[3, {4, 4}],
                           ConstantArray[2, {3, 3}], ConstantArray[1, {2, 2}]}];][[1]]
   0.000406914

MatrixPlot[tst, MaxPlotPoints -> Infinity]