One convenient way to think of Flatten with the second argument is that it performs something like Transpose for ragged (irregular) lists. Here is a simple example:
In[63]:= Flatten[{{1,2,3},{4,5},{6,7},{8,9,10}},{{2},{1}}]
Out[63]= {{1,4,6,8},{2,5,7,9},{3,10}}
What happens is that elements which constituted level 1 in the original list are now constituents at level 2 in the result, and vice versa. This is exactly what Transpose does, but done for irregular lists. Note however, that some information about positions is lost here, so we can not directly inverse the operation:
In[65]:= Flatten[{{1,4,6,8},{2,5,7,9},{3,10}},{{2},{1}}]
Out[65]= {{1,2,3},{4,5,10},{6,7},{8,9}}
To have it reversed correctly, we'd have to do something like this:
In[67]:= Flatten/@Flatten[{{1,4,6,8},{2,5,7,9},{3,{},{},10}},{{2},{1}}]
Out[67]= {{1,2,3},{4,5},{6,7},{8,9,10}}
A more interesting example is when we have deeper nesting:
In[68]:= Flatten[{{{1,2,3},{4,5}},{{6,7},{8,9,10}}},{{2},{1},{3}}]
Out[68]= {{{1,2,3},{6,7}},{{4,5},{8,9,10}}}
Here again, we can see that Flatten effectively worked like (generalized) Transpose, interchanging pieces at the first 2 levels. The following will be harder to understand:
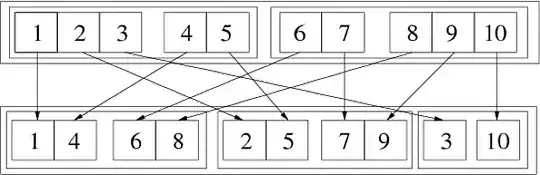
In[69]:= Flatten[{{{1, 2, 3}, {4, 5}}, {{6, 7}, {8, 9, 10}}}, {{3}, {1}, {2}}]
Out[69]= {{{1, 4}, {6, 8}}, {{2, 5}, {7, 9}}, {{3}, {10}}}
The following image illustrates this generalized transpose:
We may do it in two consecutive steps:
In[72]:= step1 = Flatten[{{{1,2,3},{4,5}},{{6,7},{8,9,10}}},{{1},{3},{2}}]
Out[72]= {{{1,4},{2,5},{3}},{{6,8},{7,9},{10}}}
In[73]:= step2 = Flatten[step1,{{2},{1},{3}}]
Out[73]= {{{1,4},{6,8}},{{2,5},{7,9}},{{3},{10}}}
Since the permutation {3,1,2} can be obtained as {1,3,2} followed by {2,1,3}. Another way to see how it works is to use numbers which indicate the position in the list structure:
Flatten[{{{111, 112, 113}, {121, 122}}, {{211, 212}, {221, 222, 223}}}, {{3}, {1}, {2}}]
(*
==> {{{111, 121}, {211, 221}}, {{112, 122}, {212, 222}}, {{113}, {223}}}
*)
From this, one can see that in the outermost list (first level), the third index (corresponding the third level of the original list) grows, in each member list (second level) the first element grows per element (corresponding to the first level of the original list), and finally in the innermost (third level) lists, the second index grows, corresponding to the second level in the original list. Generally, if the k-th element of the list passed as second element is {n}, growing the k-th index in the resulting list structure corresponds to increasing the n-th index in the original structure.
Finally, one can combine several levels to effectively flatten the sub-levels, like so:
In[74]:= Flatten[{{{1,2,3},{4,5}},{{6,7},{8,9,10}}},{{2},{1,3}}]
Out[74]= {{1,2,3,6,7},{4,5,8,9,10}}
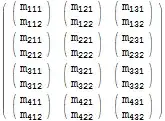
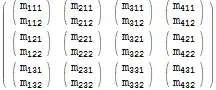







Flattenwere generalized to accept a function to apply when flattening (contracting) indices, that would be an excellent start to "tensor algebra in a can". – WReach Nov 17 '12 at 17:50Flatten[$m, {{1}, {2, 3}}]instead of Map Flatten over some level. It would be nice ifFlattenaccepted negative arguments to do that. So this case could be write likeFlatten[$m, -2]. – Murta Nov 17 '12 at 22:01the name of variblehas aprefix symbol$? – xyz Sep 16 '14 at 02:35Flattenwith the help of reading yourprefect tutorialfour times. Thanks sincerely!! :-) – xyz Sep 18 '14 at 13:12$m = Array[Subscript[m, Row[{##}]]&, {4, 3, 2}]; $m // MatrixForm. If we just want to remove the inner brace(), what should we do? Same matrix just without the inner braces – L.K. Feb 05 '17 at 19:17Flatten[$m, {{1, 3}, {2}}]– WReach Feb 06 '17 at 01:00TransposeorReversemay still be required to get all elements in the right place. For exampleTranspose[ Flatten[$m, {{1,3},{2}}] ] // MatrixForm. – Romke Bontekoe Oct 01 '21 at 08:38Flattencannot perform generalized reversals, butTranspose[Flatten[$m, {{1,3},{2}}]] === Flatten[$m, {{2},{1,3}}]– WReach Oct 01 '21 at 18:09