1

Here is an integrand

 integrand = Cos[x] Sin[x]^2 Cos[n x];

One can see it is not zere for all integer positive n as follows

 Table[Integrate[integrand, {x, 0, 2 Pi}], {n, 1, 5}]

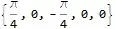
Mathematica graphics

However, when called like this Integrate gives zero

 Assuming[Element[n, Integers] && n > 0,Integrate[integrand, {x, 0, 2 Pi}]]

Mathematica graphics

This seems to be related to Mathematica giving a general result, rather than specific result? But I think it is a little misleading. Since the result is not valid for all n>0.

Should Mathmatica have given zero above? Is there a way to tell Mathematica not to do this? Does your version of Mathematica give zero as well?

Mathematica 11.2 on windows.

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • 1
    related I'm pretty sure I've seen a dupe here but did not find it yet. edit Oh, that was the one I was thinking about: 165991. I'm pretty sure you've seen it before :) – anderstood Mar 02 '18 at 00:06
  • @anderstood that is why I seem to remember I've had this problem before. But I forgot. But notice that none of the answers given are really satisfactory in general. This is because they require the user to always suspect the result from Integrate is not valid and to do special post processing. But this is not the way to do CAS. Is one supposed to see the result is not valid in general each time and handle it in special way? The best solution is that Integrate itself to always give the correct answer. I do not think 0 is correct answer here. – Nasser Mar 02 '18 at 00:54
  • I get the impression that essentially the same question is being asked in multiple guises. Is there some expectation that the answer might change? (I suppose at some point the answer might indeed change but that would be mentioned in release notes.) – Daniel Lichtblau Mar 02 '18 at 19:15
  • @DanielLichtblau I have forgotten about earlier question. As a user, one can't expect to remember each problem they encounter could be similar to one they encountered long time ago. So I asked. I also think Integrate should not return zero in these cases. Better to return no answer than an answer which is not valid as in this case. – Nasser Mar 03 '18 at 00:11
  • 1
    Returning no result instead of a generically correct result would be a really bad thing to do. – Daniel Lichtblau Mar 03 '18 at 15:51
  • 1
    I'll note that a similar problem happens with FourierCosCoefficient[]: FourierCosCoefficient[Cos[x] Sin[x]^2, x, n, FourierParameters -> {-1, 1}] returns 0 without any indication that something's amiss, even if one obtains different results for $n=1$ and $n=3$. – J. M.'s missing motivation Mar 04 '18 at 15:54
  • @DanielLichtblau sorry I was not clear. I did not mean that Integrate[integrand, {x, 0, 2 Pi}] should not evaluate, but that Assuming[Element[n, Integers] && n > 0,Integrate[integrand, {x, 0, 2 Pi}]] returning zero is the problem. zero result is simply wrong. I used this wrong result in my other calculations and wasted long time to find what was wrong. That is why it is better not to return result, than returning wrong result. If you think Assuming[Element[n, Integers] && n > 0,Integrate[integrand, {x, 0, 2 Pi}]] returning zero is valid, I'd like to learn how that can be justified. – Nasser Mar 04 '18 at 18:48
  • (1) Even with the assumptions, the result remains generically correct. (2) The issue has more to do with Simplify than Integrate per se, the latter just happens to use the former. `In[324]:= Assuming[Element[n, Integers], Simplify[Sin[n*Pi]/n]]

    Out[324]= 0(3) I'm pretty sure I've commented in past about the issues involved in usingAssumingvsAssumptions->...and also the issue of making discrete-valuedElement` assumptions. This is an area where improvements might be made, but that's by no means a given.

     – Daniel Lichtblau Mar 04 '18 at 20:40

1 Answers1

2

As has been stated on this site before, the use of Assuming is less safe than the use of Assumptions:

$Version
(*  "11.2.0 for Mac OS X x86 (64-bit) (September 11, 2017)"  *)

Integrate[Cos[x] Sin[x]^2 Cos[n x], {x, 0, 2 Pi}, Assumptions -> n ∈ Integers]
(*  -((2 n Sin[2 n π])/(9 - 10 n^2 + n^4))  *)

Table[Limit[%, n -> n0], {n0, 1, 5}]
(*  {π/4, 0, -(π/4), 0, 0}  *)
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Funny, I forgot I also answered 165991 along similar lines. The only difference here is the reference to Daniel Lichtblau's discussion of Assuming vs. Assumptions. – Michael E2 Mar 02 '18 at 02:36