Plot a "curved stroke" graphic

Question

I have this graphic:

But I would like this:

without the yellow curve, of course.

Unless you want a specific formula I recommend xkcd-style Plots :) — Kuba, Mar 05 '18 at 07:33
Btw.: Are you aware that you plot the same curve twice? You can use the option PlotStyle to change, e.g, line colors... — Henrik Schumacher, Mar 05 '18 at 10:53

score 16 · Answer 1 · answered Mar 05 '18 at 07:52

16

There are likely other ways, but this is one of the simplest:

curve = {x, Sqrt[x^2 + 1]};
nv = Normalize[Cross[D[curve, x]]];

With[{n = 30, h = 1/10},
    ParametricPlot[{curve, curve + h Sin[n x] nv} // Evaluate, {x, -2, 2}]]

wiggly hyperbola

answered Mar 05 '18 at 07:52

J. M.'s missing motivation

124,525
11
401
574

score 3 · Answer 2 · edited Mar 06 '18 at 00:14

This is another simple way. The idea is to plot a $\cos$ function, by changing its frequency and amplitude, you can adjust the twisting needed

f1[x_]:=Sqrt[x^2+1]
data=Table[z0= 1/10 Cos[50 x];z1=f1[x];{x,z0+z1},{x,-2,2,.02}];
Show[Plot[f1[x],{x,-2,2},AxesOrigin->{0,.7}],
         ListLinePlot[data,PlotStyle->Red]]

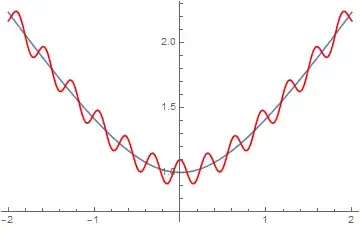
Mathematica graphics

This one has smaller frequency

data=Table[z0=1/10 Cos[20 x];z1=f1[x];{x,z0+z1},{x,-2,2,.02}];

Mathematica graphics

Manipulate[
 data = Table[z0 = h Cos[w x]; 
   z1 = f1[x]; {x, z0 + z1}, {x, -2, 2, .02}];
 Show[Plot[f1[x], {x, -2, 2}, AxesOrigin -> {0, .7}], 
  ListLinePlot[data, PlotStyle -> Red]],
 {{h, .1, "amplitude"}, 0, .5, .01, Appearance -> "Labeled"},
 {{w, 20, "frequency"}, 1, 100, 1, Appearance -> "Labeled"},
 TrackedSymbols :> {h, w},
 Initialization :>
  (
   f1[x_] := Sqrt[x^2 + 1];
   )
 ]

Plot a "curved stroke" graphic

2 Answers2