How to rotate and move plot in PolarPlot function without axes change?

Question

PolarPlot[Exp[θ], {θ, 0, 10}]  

I get plot as below:

If I need to rotate and move this object as below:

What function can I use?

I ask this question because I need to know the general method to rotate and move object. I ask a similar question about ContourPlot, it seemed there's no general method for all plot function.

Answer 1

If you use ParametricPlot[] instead, things are easier:

ParametricPlot[Composition[TranslationTransform[{-3000, -100}], RotationTransform[-120 °]][
               Exp[θ] AngleVector[θ]] // Evaluate, {θ, 0, 10}]

Note that multiplying your polar function with AngleVector[θ] (equivalently, {Cos[θ], Sin[θ]}) converts it into an equivalent form that can be used by ParametricPlot[].

Answer 2

I would say that it is not a good idea to try to apply geometric transformations to a Graphics object. One should better attack the geometric objects (the graphics primitives such as GraphicsComplex, Polygon, Line, Point, ...) inside a Graphics objects.

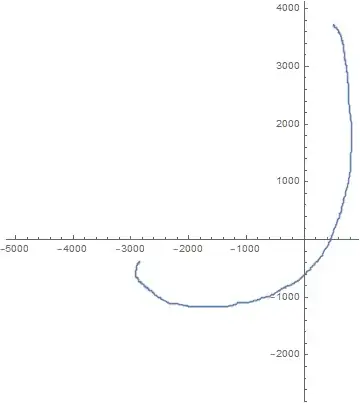
Let's start with the graphic you supplied. (Note that I specify a concise PlotRange in order to prevent myself from running into some problems with inconsistencies among the handling Options different plot types.)

g = PolarPlot[Exp[θ], {θ, 0, 10}, PlotRange -> {{-100, 100}, {-100, 100}}]

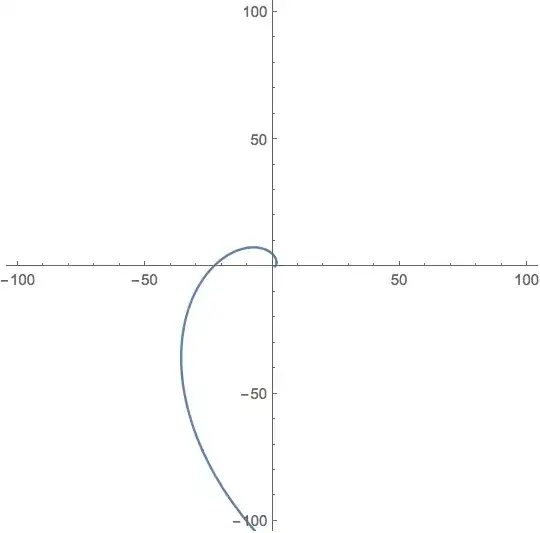
The relevant primitive here is Line as can be seen from the InputForm of g. In the following I Rotate anything that evaluates to True under RegionQ by Pi/3 about the point {0,0} and Translate it afterwards by {0,10}. Thanks to JEM_Mosig for pointing out that RegionQ can be used.

 g /. {x_?RegionQ :> Translate[Rotate[x, Pi/3, {0, 0}], {0,10}]}

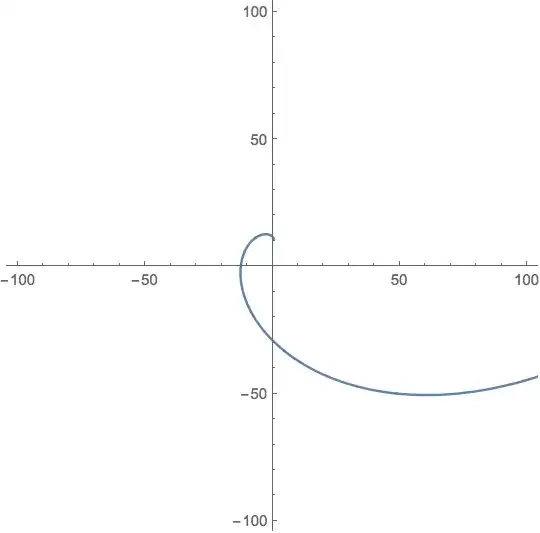
This should work with slight modifications for arbitrary plot types (also 3D plots) and for all graphics primitives.