4

I can use PolarPlot to generate a plot; however, I would like to rotate the plot by 90 degrees and then output the result using Show. Here is the code

Y20 = 
  PolarPlot[
     Abs[Sqrt[5/(16*Pi)]*(3*Cos[Theta]^2 - 1)], 
     {Theta, 0, 2*Pi}, 
     Ticks -> None
  ]
Show[Rotate[Y20, Pi/2]]

enter image description here

and the error

Show::gtype: Rotate is not a type of graphics.

If I wrap Rotate with Graphics the error message I get is

Graphics is not a Graphics primitive or directive.

Any comments will be welcomed.

Kuba
  • 136,707
  • 13
  • 279
  • 740
user13206
  • 61
  • 1

1 Answers1

5

About Rotate

Rotate is a quite strightforward function; it does what you want.

You use Rotate on something that is not a Graphics primitive? No problem, it will give what you ask:

Rotate[longvariablename, Pi/2]

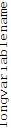
enter image description here

More formally it performs context sensitive typesetting:

ToBoxes @ Graphics @ Rotate[Disk[], Pi]
ToBoxes @ Rotate[Disk[], Pi]

GraphicsBox[
     GeometricTransformationBox[ DiskBox[{0, 0}], {{{-1, 0}, {0, -1}}, Center}]
]

RotationBox[
    RowBox[{"Disk", "[", RowBox[{"{", RowBox[{"0", ",", "0"}], "}"}], "]"}], 
    BoxRotation -> 3.14159
]

Moreover, Rotate/GeometricTransformation can't be used directly with Graphics, only with graphics primitives, that is why you get an error. You result produces something which can be boiled down to:

Graphics[{Graphics[Disk[]]}]

Your case

Y20 is not a graphics primitive so it will be treated as above. So you see you can't pass it to Show. It's no longer just Graphics (RotationBox is created - more at the end...).

Solution

So what to do? We have to take graphics primitives from Y20, Rotate them and put back into Graphics.

You can read for example How to examine structure of graphics to learn more but usually it is simple; for example, Plots and friends (with exclusion of Graphs) are producing:

 Graphics[{primitives..}, options..] (*or, for more complicated like ContourPlot*)

 Graphics[GraphicsComplex[spec...], options..] (*Normal[] can convert it back to simple form*)

for both cases first argument is what you need. Everything is an expression so it is again straightforward:

Graphics @ Rotate[First @ Y, Pi/2, {0,0}] 
(*so exactly what I've said we need to do, take-rotate-put back*)

Show takes Graphics so you can combine it with whatever you want:

Show[{
      Plot[Sin[x], {x, -1, 1}, PlotStyle -> Red],
      Graphics[Rotate[Y20[[1]], Pi/2, {0, 0}]]},
     PlotRange -> 1, AspectRatio -> Automatic, BaseStyle -> {18, Bold, Thick}]

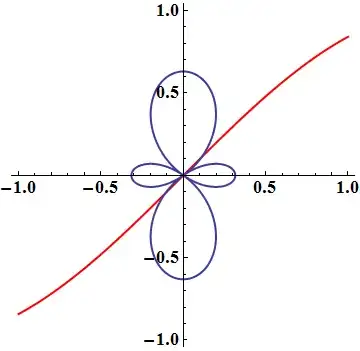
enter image description here

Keep in mind that Show, as said in documentation, takes its Options from the first argument, here Plot. It doesn't matter for this context, just pointing it out. More here

Kuba
  • 136,707
  • 13
  • 279
  • 740
  • I didn't want to say more about creating graphics because I'm not informed enough. Not very important for the context too but if anyone want, it would be nice addition. – Kuba Mar 25 '14 at 23:34