Applying an ArrayPlot as a texture to the surface of a cylinder

Question

I would like to apply a matrix plot to the surface of a 3D cylinder. The matrix plot is the output from a custom cellular-automata, and it would be nice to see the lefthand side of the plot connected to the righthand side.

Edit

This is the solution I ended up using:

mrt =
  ArrayPlot[CellularAutomaton[30, RandomInteger[{0, 1}, 100], 30],
    Frame -> False,
    ImagePadding -> 0,
    PlotRangePadding -> 0];
ParametricPlot3D[{Sin[t]/2Pi, Cos[t]/2Pi,u},{t,0,2Pi},{u,0,2},
  Boxed -> False,
  Axes -> False,
  PerformanceGoal -> "Quality",
  ImageSize -> {300, 300},
  Lighting -> "Neutral",
  PlotStyle -> Texture[mrt],
  Mesh -> None,
  ViewPoint -> {0, 3, 1}]

enter image description here

I'm tempted to call this a duplicate of On coloring the faces of a surface differently with parameter-dependent colors because all the methods are covered there (except for how to draw a cylinder). — Jens, Dec 29 '12 at 22:20
As kguler has pointed out in the answer the principle of "Wrapping a rectangle to form a cylinder" has also been answered, sorry for the duplicate — si-tacuisses, Dec 29 '12 at 23:20

score 14 · Accepted Answer · edited Apr 13 '17 at 12:55

You can use the raster image produced by MatrixPlot as Texture directive if you construct Cylinder using ParametricPlot3D or ContourPlot3D.

 mplt = MatrixPlot[Table[Sin[x y/100], {x, -10, 10}, {y, -10, 10}], 
 ColorFunction -> "Rainbow", Frame -> False, ImagePadding -> 0, 
 PlotRangePadding -> 0]

enter image description here

ParametricPlot3D

 ParametricPlot3D[{Cos[theta], Sin[theta], rho}, {theta, -Pi, Pi}, {rho, 0, 2}, 
 PlotStyle -> Directive[Specularity[White, 30], Texture[mplt]], 
 TextureCoordinateFunction -> ({#1, #3} &), Lighting -> "Neutral", 
 Mesh -> None, PlotRange -> All, TextureCoordinateScaling -> True]

enter image description here

Update: To wrap the matrix plot around the cylinder

Change the setting for TextureCoordinateFunction to

TextureCoordinateFunction -> ({#4, #5} &)  (*Thanks: @Rahul *)

enter image description here

Or leave out the TextureCoordinate... options out and use PlotStyle -> Texture[mplt] (thanks: @DROP TABLE):

ParametricPlot3D[{Cos[theta], Sin[theta], rho}, {theta, -Pi, Pi}, {rho, 0, 2},
 PlotStyle -> Texture[mplt], Lighting -> "Neutral", Mesh -> None, 
  PlotRange -> All, ImageSize -> 400]

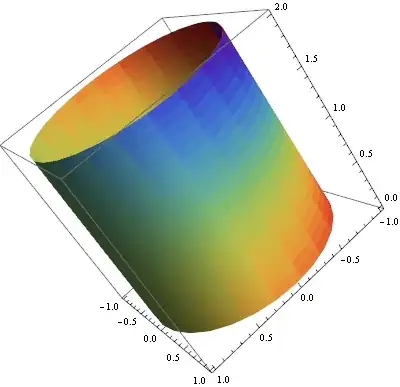
enter image description here

ContourPlot3D

ContourPlot3D[x^2 + y^2 == 1, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, 
 Mesh -> None, Lighting -> "Neutral", 
 ContourStyle -> Directive[Specularity[White, 30], Texture[mplt]], 
 TextureCoordinateFunction -> ({#1, #3} &)]

enter image description here

Thanks this looks great exactly what I was looking for. Great Idea to use a parametric plot instead of Graphics Primitive. — si-tacuisses, Dec 29 '12 at 23:01
It looks like you're projecting the texture on the $(x,z)$ coordinates, while I think the OP wants it to wrap around the cylinder along $(\theta,\rho)$. For the parametric plot, that would be TextureCoordinateFunction -> ({#4, #5} &). — , Dec 29 '12 at 23:43
The given answer by kguler did not exactly answer my question since the texture is duplicated, however the answer and the link to "Wraping a Rectangle to Form a Cylinder" have solved my problem. I ended up using: ParametricPlot3D[{Sin[t]/2 Pi, Cos[t]/2 Pi, u}, {t, 0, 2 Pi}, {u, 0, 2}, Axes -> False, ImageSize -> {300, 300}, Lighting -> "Neutral", PlotStyle -> Texture[mrt], Mesh -> None] — si-tacuisses, Dec 30 '12 at 00:27

amr · Answer 2 · 2012-12-30T03:35:16.487

I made a program of this kind before and the most efficient solution I found was Cuboid. Or perhaps it was the best-looking solution. The rendering code is:

render[stack_, iterations_, color_, thickness_, overlap_] := Module[
    {center, interval, width = Length[stack[[1]]]},
    interval = 2. \[Pi]/width;

    Last@Reap[Do[
      Sow[Rotate[
        Last@Reap[Do[
           If[stack[[level, rad]] == 1,

            center = {Cos[interval*rad]/interval, 
               Sin[interval*rad]/interval, 0} // N;

            Sow[Cuboid[
              center + {0, 0, -level} + {thickness, overlap/2 + .52, .52}, 
              center + {0, 0, -level} - {0, overlap/2 + .52, .52}], color];
            (*make the cylinder darker on the inside*)
            Sow[Cuboid[
              center + {0, 0, -level} + {0, overlap/2 + .52, .52}, 
              center + {0, 0, -level} - {.02, overlap/2 + .52, .52}], 
             Darker[color, .5]]],
           {level, 1, iterations}], _, {#1, #2} &],
        interval*rad, {0, 0, 1}, center]]

      , {rad, 1, width}]]
   ];

It just goes through the matrix, and if there is a 1 it Sows the proper Cuboid. Note the Rotate, which rotates an entire column's worth of cells (columns are parameterized by rad).

The renderings look like:

enter image description here

By changing thickness you can also render the blocks as wafers to get a nice cylindrical look.

Wow. This looks awesome! – si-tacuisses Dec 30 '12 at 10:44 — si-tacuisses, Dec 30 '12 at 10:44

C. E. · Answer 3 · 2015-05-11T01:13:07.277

4

I have an implementation of something like this. I might as well post it.

The cylinder is made up of square polygons.
coordinates lists all the corners of all the polygons at a certain height.
layer takes the coordinates of the corners and generates the polygon required for one row in the cylinder.
pieces generates all the rows.

Code:

coordinates[z_, n_, h_] := Riffle[
  Append[z] /@ CirclePoints[n],
  Append[z + h] /@ CirclePoints[n]
  ]

layer[n_, z_, data_] := GraphicsComplex[
  coordinates[z, n, 2 Pi/n],
  Polygon[# + {0, 1, 3, 2} /. {(2 n + 1) -> 1, (2 n + 2) -> 2}] & /@ 
   Pick[Range[1, 2 n, 2], data, 1]
  ]

pieces[n_, nrOfLayers_] := MapThread[
  layer[n, #, #2] &, {
    2 Pi Range[nrOfLayers]/n,
   Most@CellularAutomaton[30, RandomChoice[{0, 1}, n], nrOfLayers]
   }]

Graphics3D[
 pieces[200, 50],
 AspectRatio -> 1
 ]

Example output: Example

Different colors can be given for the inside and the outside:

Graphics3D[{
  FaceForm[Blue, Yellow],
  pieces[200, 50]
  },
 AspectRatio -> 1
 ]

Mathematica graphics

edited May 11 '15 at 01:13

answered May 11 '15 at 01:01

C. E.

70,533
6
140
264

I think I recall a question along these lines in the last few days. Did that one end up getting closed as a duplicate of this one? – MarcoB May 11 '15 at 05:23
@MarcoB not yet: 83112 – Kuba May 11 '15 at 06:48
@Kuba I suspect that might happen soon then ;-) This whole series of answers fits that question very closely. – MarcoB May 11 '15 at 06:53
@MarcoB I think so, and +1 @ Pickett :) – Kuba May 11 '15 at 06:53

score 3 · Answer 4 · answered Apr 11 '13 at 06:25

Instead of using ArrayPlot[], one might want to use Image[] directly to produce the textures. For instance, here is the CA texture:

BlockRandom[SeedRandom[42, Method -> "MersenneTwister"]; (* for reproducibility *)
            ca30 = CellularAutomaton[30, RandomInteger[{0, 1}, 100], 30];]

(* Image[]'s convention is the reverse of ArrayPlot[]'s *)
tex = Image[1 - ca30, ImageSize -> Large];

ParametricPlot3D[{2 Cos[u], 2 Sin[u], z}, {u, -π, π}, {z, 0, 2},
                 Axes -> None, Boxed -> False, Lighting -> "Neutral",
                 Mesh -> None, PlotStyle -> Texture[tex]]

CA on a cylinder

Here's a colorful example:

tex2 = Colorize[Image[Rescale[
        N[Table[Sin[π x/10 + Sin[π y/10]], {x, 0, 20}, {y, 0, 40}]]], ImageSize -> Large],
                ColorFunction -> "Rainbow"];

ParametricPlot3D[{Cos[u], Sin[u], z}, {u, -π, π}, {z, 0, 2}, 
                 Axes -> None, Boxed -> False, Lighting -> "Neutral",
                 Mesh -> None, PlotStyle -> Texture[tex2]]

colorful sine on a cylinder

Applying an ArrayPlot as a texture to the surface of a cylinder

Edit

4 Answers4

ParametricPlot3D

ContourPlot3D

Related:

Linked

Related