I would like to show the current distribution in a thin cylinder in 3D. The figure below shows the open cylinder.
I am trying to use that figure as a texture in a 3D plot inspired by this answer.
scalarField[r_, \[Phi]_, z_] :=
1/Pi*(z + 2*Sum[Sinh[n*z]/Cosh[n*3]/n*Cos[n*\[Phi]], {n, 1, 33}]);
contourTexture =
ContourPlot[
scalarField[1, \[Phi], z], {z, \[Phi]} \[Element]
Rectangle[{-3, -Pi}, {3, Pi}], AspectRatio -> 1/2, Frame -> False];
streamTexture =
StreamPlot[{-D[scalarField[1, \[Phi], z], z], -D[
scalarField[1, \[Phi], z], \[Phi]]}, {z, \[Phi]} \[Element]
Rectangle[{-3, -Pi}, {3, Pi}], AspectRatio -> 1/2,
Evaluated -> True, Frame -> False, StreamStyle -> Black];
rev = RevolutionPlot3D[{1, t}, {t, -3, 3},
TextureCoordinateFunction -> ({#1, #2} &),
PlotStyle -> Texture[contourTexture + streamTexture]];
Show[rev]
The output I am getting is:
Two points I don't know:
- What to pass as
TextureCoordinateFunction - if the calling
PlotStyle -> Texture[contourTexture + streamTexture]is correct
I have also seen this question, but I can't figure out how to adapt it.

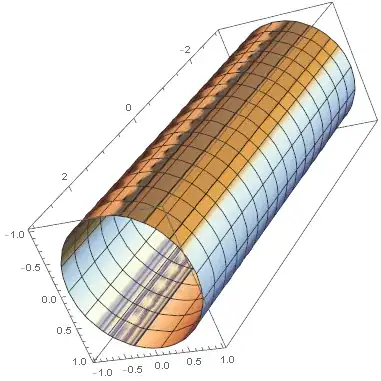
RevolutionPlot3D[{1, t}, {t, -3, 3}, TextureCoordinateFunction -> ({#4, #5} &), PlotStyle -> Texture[ Show[contourTexture, streamTexture, PlotRangePadding -> None]], Lighting -> "Neutral"]– Kuba Jun 07 '17 at 17:19#4and#5are inTextureCoordinateFunction -> ({#4, #5} &)? – Pedro H. N. Vieira Jun 07 '17 at 17:33