5

I am trying to solve a system of recurrence relations as follows.

RSolve[{a[p] == 1 + (2/n) b[p - 1] + ((p - 1)/n) a[p - 1], 
        b[p] == 1 + (p/n) b[p - 1], 
        a[1] == 1 + 2/n, 
        b[0] == 1}, 
     {a[p], b[p]}, p]

Having done this, I would like to set $p=n-1$ and then plot the resulting functions $a[n-1]$ and $b[n-1]$ for $n=1, ..., 1000$.

I am failing at the first hurdle as Mathematica version 8 just returns the RSolve line when I press shift-enter.

Update. Following a request for an example using Maple 16. I do the following.

rsolve({a(1) = 1+2/n, a(p) = 1+(p-1)*a(p-1)/n+2*b(p-1)/n, b(0) = 1, b(p) = 1+p*b(p-1)/n}, {a(p), b(p)});
subs(p = n-1, %);

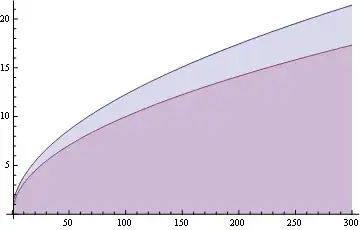
I then copy the result for a(n-1) and plot it

plot([seq([n, (1/n)^(n-1)*n*GAMMA(n-1)*(Sum((n+2*(1/n)^p1*exp(n)*GAMMA(p1+1, n))/(n^2*(1/n)^(p1+1)*GAMMA(p1+1)), p1 = 1 .. n-2)+1+2/n)], n = 2 .. 200)], style = point);

This gives

enter image description here

Simd
  • 1,119
  • 1
  • 7
  • 17
  • 1
    First issue is the syntax : RSolve with capital S. – b.gates.you.know.what Jan 01 '13 at 19:30
  • Strongly related http://mathematica.stackexchange.com/q/16919/193 – Dr. belisarius Jan 01 '13 at 19:41
  • Sorry... copy and paste error. I have the same problem with RSolve with a capital S. Is there a way to restart so that there are no existing function/variable settings or is there some other reason it doesn't appear to do anything? – Simd Jan 01 '13 at 19:48
  • 1
    solving for b[p] seperately produces a solution for b : solb = RSolve[{b[p] == 1 + (p/n)*b[p - 1], b[0] == 1}, b, p][[1, 1]]. Substituting this in the other equation seems to be more complicated though sola = RSolve[{a[p] == 1 + (2/n)*b[p - 1] + ((p - 1)/n)*a[p - 1], a[1] == 1 + 2/n} /. solb, a, p] – Thies Heidecke Jan 01 '13 at 19:53

1 Answers1

5

In two steps, since they can be decoupled:

h1 = RSolve[{
   b[p] == 1 + (p/n) b[p - 1],
   b[0] == 1}, {b[p]}, p]
h2 = RSolve[{
   a[p] == Evaluate[b[p] /. h1[[1]]] + ((p - 1)/n) a[p - 1],
   a[1] == 1 + 2/n}, {a[p]}, p]

DiscretePlot[{b[i] /. Evaluate[h1 /. p -> n - 1 /. n -> i + 1], Sqrt[i]}, {i, 300}]
DiscretePlot[ a[i] /. Evaluate[h2 /. p -> n - 1 /. n -> i + 1], {i, 300}]

Comparing b[i]with Sqrt[i]

Mathematica graphics

And this is a[i]

Mathematica graphics

Edit

BTW, answering your comment

Thanks. How can I now do the substitution and plotting? If there isn't a bug then it should look like $sqrt(n)$

here is a reasonable approximation to b[i] using Sqrt[]: 

y[i_] := Sqrt@(1.78081659706051 + 1.57076044099885*i) - 0.332147990949542; 
DiscretePlot[Evaluate[b[p] /. h1[[1]] /. p -> n - 1 /. n -> i + 1] - y[i], {i,10000}, 
             PlotRange -> All]

Mathematica graphics

Or, if you want an exact result:

b[n] -> E^n n ExpIntegralE[1 - n, n]
Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
  • Thanks. How can I now do the substitution and plotting? If there isn't a bug then it should look like $\sqrt{n}$. – Simd Jan 01 '13 at 19:56
  • Thanks but isn't it possible to use the answer to RSolve[{ a[p] == Evaluate[b[p] /. h[[1]]] + ((p - 1)/n) a[p - 1], a[1] == 1 + 2/n}, {a[p]}, p] without having to retype the answer for a[n]? – Simd Jan 01 '13 at 20:04
  • @lip1 Look at it now – Dr. belisarius Jan 01 '13 at 20:13
  • @belisarius Don't you think Mathematica should be able to solve it the way you did ? – b.gates.you.know.what Jan 02 '13 at 07:59
  • @b.gatessucks RSolve[] functionality is still cutting its teeth – Dr. belisarius Jan 02 '13 at 16:09
  • @belisarius Are you sure the plot of a[n-1] is correct? Here is what I do in Maple and I get a different graph.rsolve({a(1) = 1+2/n, a(p) = 1+(p-1)a(p-1)/n+2b(p-1)/n, b(0) = 1, b(p) = 1+p*b(p-1)/n}, {a(p), b(p)});

    subs(p = n-1, %);

    I then copy the answer for a(n-1) and do plot([seq([n, (1/n)^(n-1)nGAMMA(n-1)(Sum((n+2(1/n)^p1exp(n)GAMMA(p1+1, n))/(n^2(1/n)^(p1+1)GAMMA(p1+1)), p1 = 1 .. n-2)+1+2/n)], n = 2 .. 200)], style = point)

     – Simd Jan 03 '13 at 11:43
  • @belisarius In fact it should look like $\sqrt{\frac{\pi}{2} n}$ in the limit. – Simd Jan 03 '13 at 11:57
  • @lip1 b[n] behaves like Sqrt[Pi/2 n] when n->Infinity, yes – Dr. belisarius Jan 03 '13 at 13:12
  • @lip1 Please post an image, I haven't Maple available here now. – Dr. belisarius Jan 03 '13 at 13:13
  • @lip1 I cross checked the plot for a[i] and seems right – Dr. belisarius Jan 03 '13 at 13:29
  • @belisarius I mean a[n-1] behaves like $\sqrt{\frac{\pi}{2} n}$. – Simd Jan 03 '13 at 13:30
  • Are you completely sure? because it's b[n] the one that behaves EXACTLY like that – Dr. belisarius Jan 03 '13 at 13:31
  • @belisarius See update. – Simd Jan 03 '13 at 13:47
  • @belisarius I got downvoted for posting the picture! – Simd Jan 03 '13 at 14:11
  • 1
    @lip1 No, you haven't got downvoted. I removed my upvote until you put some more work on your question. You have now two expressions that pretend to solve your problem. I suggest replacing that expressions back into the original equations and see if both of them comply. – Dr. belisarius Jan 03 '13 at 14:23