How to mesh two ParametricPlot3D function and change the line to cuboid

Question

Show[ParametricPlot3D[{Sin[u], Cos[u], u}, {u, 0, 2}, 
      PlotStyle -> Directive[Red, Thick], PlotRange -> All], 
     ParametricPlot3D[{2 Sin[u], 2 Cos[u], u}, {u, 0, 2}, 
      PlotStyle -> Directive[Black, Thick], PlotRange -> All]]

Hi experts,

I would like to ask:

1) How to make the line be replaced with cuboid so that we can see how it's twisted? I did replace the line with tube, but I cant see how the line is twisted:

2) What if we want to mesh the two lines with seperate ParametricPlot3D as shown above (This is just an example)?

Your answer is appreciated.

What do you mean by "twisted"? Do you want to visualize the Frenet frame? — Henrik Schumacher, Apr 27 '18 at 06:08
Instead of visualize Frenet Frame, how i wish is to enlarge the curve (in cuboid shape) to see how the curve is twisted. — VTeh, Apr 27 '18 at 06:13
Possible duplicate: https://mathematica.stackexchange.com/questions/69831/moving-polygon-on-path-curve-to-create-3d-shape — Michael E2, Oct 12 '18 at 10:36

Henrik Schumacher · Answer 1 · 2018-10-12T06:28:43.110

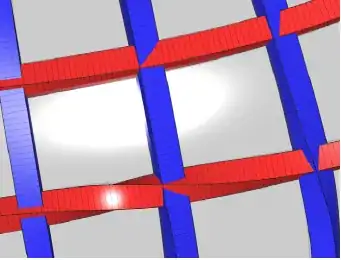
Maybe this is what you ask for. It used the Frenet frame of a curve in order to map the corners of a square into $\mathbb{R}^3$. Afterwards, these points are connected to form a tube with rectangular cross section.

curve = t \[Function] {Sin[t], Cos[t], t};
tangent = t \[Function] Evaluate[Simplify[curve'[t]/Sqrt[curve'[t].curve'[t]]]];
normal = t \[Function] Evaluate[Simplify[tangent'[t]/Sqrt[tangent'[t].tangent'[t]]]];
binormal = t \[Function] Evaluate[Cross[tangent[t], normal[t]]];

radius = 0.2;
crosssection0 = radius {{1, 1}, {-1, 1}, {-1, -1}, {1, -1}};
crosssection = t \[Function] Evaluate[crosssection0.{normal[t], binormal[t]}];
tlist = Subdivide[0., 2. Pi, 1000];

pts = Flatten[Plus[
    Transpose[
     ConstantArray[curve /@ tlist, Length[crosssection0]], {2, 1, 
      3}],
    (crosssection /@ tlist)
    ], 1];
m = Length[crosssection0];
n = Length[tlist];
polys = Partition[Flatten[BlockMap[
     Transpose[{Partition[#[[1]], 2, 1, #[[1, 1]]], 
        Reverse /@ Partition[#[[2]], 2, 1, #[[2, 1]]]}] &,
     Transpose[Table[Range[i, m n, m], {i, 1, m}]],
     2, 1
     ]], 4];

gc = GraphicsComplex[pts, {
   FaceForm[Orange, Darker@Darker@Blue], 
   Specularity[White, 30], EdgeForm[], Polygon[polys]
  }];
Graphics3D[
 gc, 
 Lighting -> "Neutral"
 ]

You can do that also with other cross sections. For example,

crosssection0 = Times[
   CirclePoints[10.],
   Flatten[Transpose[{
      ConstantArray[radius, 5],
      ConstantArray[0.5, 5]
      }]]
   ];

leads to

Edit

I packaged everything into a simple function.

ClearAll[plot]
plot[curve_, tlist_, radius_, OptionsPattern[{
    PlotStyle -> {},
    "CrossSection" -> {{1, 1}, {-1, 1}, {-1, -1}, {1, -1}}
    }]] := 
 Module[{tangent, normal, binormal, crosssection, crosssection0, pts, 
   m, n, polys, gc},
  tangent = 
   t \[Function] Evaluate[Simplify[curve'[t]/Sqrt[curve'[t].curve'[t]]]]; 
  normal = t \[Function] 
    Evaluate[Simplify[tangent'[t]/Sqrt[tangent'[t].tangent'[t]]]]; 
  binormal = t \[Function] Evaluate[Cross[tangent[t], normal[t]]];
  crosssection0 = N[OptionValue["CrossSection"]];
  crosssection = 
   t \[Function] 
    Evaluate[radius crosssection0.{normal[t], binormal[t]}];

  pts = Flatten[
    Plus[
     Transpose[ConstantArray[curve /@ tlist, Length[crosssection0]], {2, 1, 3}], 
     (crosssection /@ tlist)
     ], 
    1];
  m = Length[crosssection0];
  n = Length[tlist];
  polys = 
   Partition[
    Flatten[BlockMap[
      Transpose[{Partition[#[[1]], 2, 1, #[[1, 1]]], 
         Reverse /@ Partition[#[[2]], 2, 1, #[[2, 1]]]}] &, 
      Transpose[Table[Range[i, m n, m], {i, 1, m}]], 2, 1]], 4];

  gc = GraphicsComplex[
    pts, {FaceForm[Orange, Darker@Darker@Blue], 
     Specularity[White, 30], EdgeForm[], 
     Sequence @@ Flatten[{OptionValue["PlotStyle"]}], Polygon[polys]}];
  Graphics3D[gc, Lighting -> "Neutral"]
  ]

Now you can do things like this:

tlist = Subdivide[0., 2. Pi, 250];
img = Import["https://i.stack.imgur.com/wtJoA.png"];
img = Binarize[img~ColorConvert~"Grayscale"~ImageResize~500~Blur~3];
pts = DeleteDuplicates@
   Cases[Normal@
      ListContourPlot[Reverse@ImageData[img], 
       Contours -> {0.5}], _Line, -1][[1, 1]];
center = Mean@MinMax[pts] & /@ Transpose@pts;
pts = # - center & /@ pts[[;; ;; 20]];


Show[
 plot[u \[Function] {Sin[u], Cos[u], u}, tlist, 0.15,
  "CrossSection" -> 0.01 Reverse[pts],
  PlotStyle -> FaceForm[Pink, Blend[{Red, Blue}, 0.5]]
  ],
 plot[u \[Function] {2 Sin[u], 2 Cos[u], u}, tlist, 0.2]
 ]

I got the elephant from this post by anderstood.

How about meshing two ParametricPlor3D curves as shown above? — VTeh, Apr 27 '18 at 07:15
I don't know of a built-in way to do it with, e.g. ParametricPlot3D. But Graphics3D is what is internally used in all 3D plots. — Henrik Schumacher, Apr 27 '18 at 07:20

score 3 · Answer 2 · answered Oct 12 '18 at 11:01

It's unclear from the image what sort of twisting is desired. The image in the OP, to my eye, does not reflect the torsion of the Frenet Frame. In any case, here is a way using Tube with the method option "TubePoints" -> 4 to get a square cross section (see, for example, here):

ParametricPlot3D[{Sin[u], Sin[2 u], u/5 Cos[u]}, {u, 0, 10},
  PlotStyle -> Red, PlotRange -> All, Method -> {"TubePoints" -> 4}
  ] /. Line[p_] :> Tube[p, 0.2]

Mathematica graphics

Here's a mesh of a torus (zoomed in image shown):

Show[
  ParametricPlot3D[Evaluate@
    Table[{4 + (3 + Cos[v]) Sin[u], 4 + (3 + Cos[v]) Cos[u], 
        4 + Sin[v]} /. {u -> 2 u, v -> u + 3 v} // Evaluate,
     {v, 0, Pi, Pi/8}],
   {u, 0, 2 Pi}, PlotStyle -> Directive[Red, Thick], PlotRange -> All,
    Method -> {"TubePoints" -> 4}],
  ParametricPlot3D[Evaluate@
    Table[{4 + (3 + Cos[v]) Sin[u], 4 + (3 + Cos[v]) Cos[u], 
        4 + Sin[v]} /. {u -> 2 u - v, v -> 3 v} // Evaluate,
     {u, 0, Pi, Pi/8}],
   {v, 0, 2 Pi}, PlotStyle -> Directive[Blue, Thick], 
   PlotRange -> All, Method -> {"TubePoints" -> 4}]
  ] /. Line[p_] :> Tube[p, 0.1]

Mathematica graphics

How to mesh two ParametricPlot3D function and change the line to cuboid

2 Answers2